2020-12-25

MOAとスパムメール判別とsolafuneとatmacup参戦記

はじめに

怒涛（甘い？）のコンペラッシュが終わりしばらく経ちました。あまりコミットできなかったコンペもありますがせっかくなのでざっくりと記録を残しておきます。細かいところはnotebookを見れば思い出せるはず…それぞれの結果は以下の通りでした。

MOA（kaggle）：755位 / 4,373 teams

スパムメール判別（Probspace）：20位 / 225 teams（うち投稿88）

空港利用者数予測（Solafune）：9位 / 118 teams（うち投稿63）

MOA

Mechanisms of Action（MOA）、日本語で作用機序と呼ばれるすごく大雑把にいうと薬にどんな効果があるか予測するマルチラベルのコンペでした。自分の大好物なテーブルコンペということで飛びついたのですが、一番時間をかけたのはドメイン知識の習得かも知れません…コードより長い専用のnotebookを一つ作るくらい調べ続けてやっと何とかコンペの意味を理解することができました。

コンペ始まって1か月弱くらいしかコミットしておらず、ほぼ公開ノートの写経で10subだけして後半2か月は何もせずで終わりました。というのも、大好きなGBDTでも予測もできるのですが公開ノートのほとんどはDeepLearning手法で、後述する他のコンペでも「これはDeepLearningまじめに勉強せなあかん」となり、インプットに時間を割いていたらタイムオーバーとなった形です。。

ということでMOAで一番身についたのは「DNAとRNAの違い」とか「薬剤試験のやりかた」とか機械学習と何も関係ないところばかりが印象に残っているのですが、一応以下のことは写経しつつ学びましたのでメモ。分かってないやつは別途ちゃんと勉強したいです。

GBDTでマルチラベルを解こうとすると（DLほどでは無いにせよ）普通のテーブルデータに比べえぐい時間かかる
RankGauss
特徴選択（Variance Threshould）
scheduler（ちゃんと分かってない）
DropOutやBatchNorm（ちゃんと分かってない）
SEEDたくさんで学習・予測してアンサンブルすると良いことがある（ほぼ分かってない）
Smoothing（ほぼ分かってない）
TabNet（ほぼ分かってない）

早々に試行錯誤を諦めインプットに移行したこと自体は後悔していないのですが、自分は「問題設定は難しいしラベルの意味も分からんし何して良いか分からん」状態だったのですが、後々公開された解法を見ていると皆さん問題理解もさることながら「データの分布や最低限の意味から何をすべきかを考え出す」能力が自分とは段違いで凹みました。。LateSubもまだ全然できていないのでこのGitHubとか見ながら知見を溜めていきたいと思います。

スパムメール判別コンペ

機械学習の分類の例で良く見る、メールがSpamかHamかを二値分類するコンペでした。参加時点では自然言語処理経験ゼロだったのですが、学びのつもりで参加しました。

こちらも最初の一週間くらいは怒涛のコミットをしたのですが、後半2か月はほぼ何もできずでした…初日に早々にBaselineを作成したり元論文の訳などをトピックにしたりしたところ結構な評価を頂けたのは唯一自慢できることです。1位の方も参考にしてくださった様で、しばらくは自己肯定感高く生きられそうです。

そんな状況ではあったのですが、自然言語処理のファーストステップはこのコンペに取り組んだおかげで身についたのでとてもよかったです！テキストのベクトル化、TF-IDF、stopwordなどの前処理、wordcoludの表示方法や他にもアンダーサンプリングなどなど…。

しかし、DeepLearning以外の分類器（ナイーブベイズ、ロジスティック分類、ランダムフォレスト、SVM）のアンサンブルでスコアを高めた後、「よーし、まだ全然分からないけどRNNとかその親戚っぽいやつもやってみるぞー」となってしまい、DeepLearning勉強沼に嵌りそのまま後述のsolafuneなどに参加しているうちに終ぞこのコンペに戻ってくる暇はなく、完全にお勉強のための参加になってしまいました…。

上位の方々は全員BERTなどDeepLearning手法なのかなぁと思っていたのですが、勝敗を分けたのはpseudo-labeling（trainのSpam割合は約2%に対し、testでは約70%と公開されていた。確度高くSpamと予測したtestデータをtrainに加えることが効いた）だったようで、自分の知識でも工夫次第で上位を狙えたかもなぁというのが少し心残りです。

ゼロから作るDeepLearningを読んで記事化していたのですが、このコンペラッシュで自然言語周りだけまとめられていない＆コンペに適用できておらず身に付きがだいぶ甘いのでちゃんとアウトプットして身に着けたいと思います…！

Solafune

日本国内の空港の衛星画像からその空港の年間利用者数を予測するという、画像+回帰のコンペでした。

MOAとスパムメール判別コンペからDeepLeaningの勉強に取り組みつつ、「CNN使ってみたいけど画像コンペはどれもデータが大量で気軽に参加できないな～」と思っていたのですが、このコンペは学習＆検証＆予測用の画像合わせて150枚以下しかない、とても参加しやすいコンペでした。以下のツイートの様な事をチャレンジしていました。

#solafune 順位バグってる？けど1位と2位が最後の最後にめちゃくちゃ接戦してる…スゴい…自分のやったのは↓の感じだったのですが、解法公開する方安定した学習と検証する方法教えてください。。 pic.twitter.com/OZxvdcDrqa
— ちゃかぶ (@cha_kabu) 2020年11月30日

基本中の基本みたいなことやっただけですが、カスタムデータセットの作り方など地味だけど必須な部分は中々理論を学んでいるだけでは身につかず、その辺も写経ではなく挑戦できたのは大きかったです。

ただ、このコンペを通して「やっぱりゴリゴリGPU使うコンペはGoogleColabじゃキツそう（言わずもがな、8年前に買った我が家のPCも）」とも感じました。このデータが少ないコンペでも頻繁に「CuDAメモリ限界です」とか「君GPU使い過ぎだからいったん使用禁止な」のエラーが出たので、他のコンペは相当キツそうです。。画像コンペなりの面白さは感じとれたのですが自分はテーブルコンペがやっぱり一番好きというのも再認識できたので、課金するのも中々踏み出せず、けど忘れない程度に使わないと忘れてしまうしなー、と程よいコンペを模索中です。

atmacup08

ゲームのタイトルやプラットフォーム、発売年、評価スコアなどの情報から全世界での売上を予測する回帰のコンペでした。どのコンペも面白いのですがこのコンペは今まで参加した中で正直一番好きです。

テーブルコンペ！
タイトルに合ったとおり初心者向けで分かりやすい
かといってやることは色々ある
ディスカッションが盛ん（参加数考えたらkaggle以上？）

特に2についてはTwitterでも同じことを言っている方がいらっしゃいましたが、次世代（？）Titanicとしてとても良いと思います。

このコンペでの最大の反省はディスカッションに投稿した通り戦術を絞り過ぎた（「ほぼランダムに思えるヒット作をどうすれば予測できるか」ばかり考えていた）ことなのですが、最大の学びは運営の方含めて皆様積極的にコードを公開してくださるおかげで「つよつよの方との実装の違いを知れた」ことです。

今まで自分は自作関数やクラスはほぼ使わない＆実験管理も1コンペあたり精々3ノートに分けるくらい（自分の中で「大幅にスコア上がったな」と思えたときだけコピーを作成。根拠はなし。）、何でどんな変化が起きたかはスプレッドシートにまとめておく…という感じだったのですが、皆様とても綺麗に管理されていました。。

クラスや関数の使い方はLatesubで一通りパクらせて頂き、実験管理、Docker、GitHubあたりもUdemy等で学び中なので、次に参加するコンペではその辺整備して挑みたいと思います。特に自作クラスはまとめておくと「効くか分からないけどとりあえず適用してみるか」が気軽にできて試行の幅が広がるので積極的に増やしていきたい所存です。

終わりに

アウトプットが止まってしまっていたのでやっと書けて満足なのですが、なぜわざわざクリスマスイブの夜に書いてるんですかね…あと次のコンペ何にしようか迷い中。。

2020-11-23

ゼロから作るDeep Learning3　フレームワーク編を読む　その⑫ステップ55～58

はじめに

以下の記事シリーズの続きです。

cha-kabu.hatenablog.com

本編

ステップ55-56 CNNのメカニズム

ほとんどコードは無く、CNN自体の説明です。実装についてはステップ57でまとめて行われるので、特に苦手なところだけまとめておきます。

出力サイズの計算方法

いつも計算時にいったん考えないと出てこない…数式で書くと↓ $O = \dfrac{I + P \times 2 - F}{S}+1$

で、日本語で書くと「アウトプットのサイズは"入力サイズにパディングの2倍を足してフィルタサイズを引いたものをストライドで割って1を足して"求める」ですが、今回こちらのQiita記事の説明を見て頭に染み付いた気がします！画像借用します。

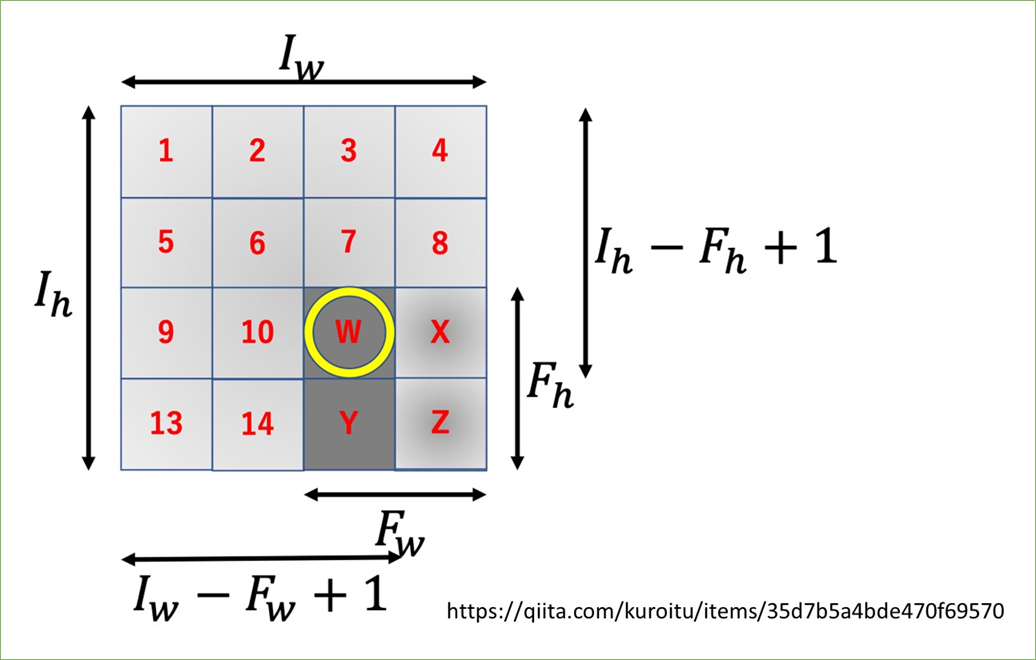
f:id:cha_kabu:20201123211755p:plain

この図が言っているのは、「（パディングやストライドを考えなければ）一番最後にフィルタを掛けた時のフィルタの左上、画像でいうとWのインデックスが出力行列のサイズになる」ということです。この場合Wは3行3列にいるので出力も3*3になります。

これをベースにしつつ、

パディングは両端が増えるから $P\times 2$ を足す
ストライドはフィルタを1マスごとにかけるのを基準にすると反比例的に回数が減っていくので $S$ で割る（ $+1$ 以外）

を思い出せば忘れずにいられそうです…！

3～４階テンソルの畳み込み演算による形状変化

分からなくはないですがこちらもパッと出てこないので書籍のまんまですがメモって覚えます。まずは3階テンソルの場合。

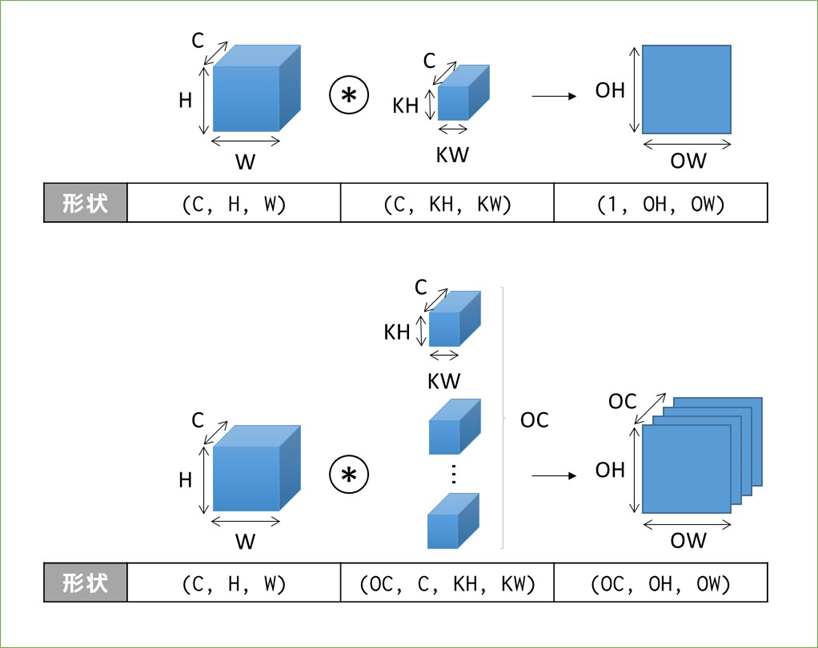
f:id:cha_kabu:20201123211815p:plain

これにバイアスが足されることもありますが、Outputのサイズは変わりません。続いて4階テンソル（ミニバッチ処理）の場合。

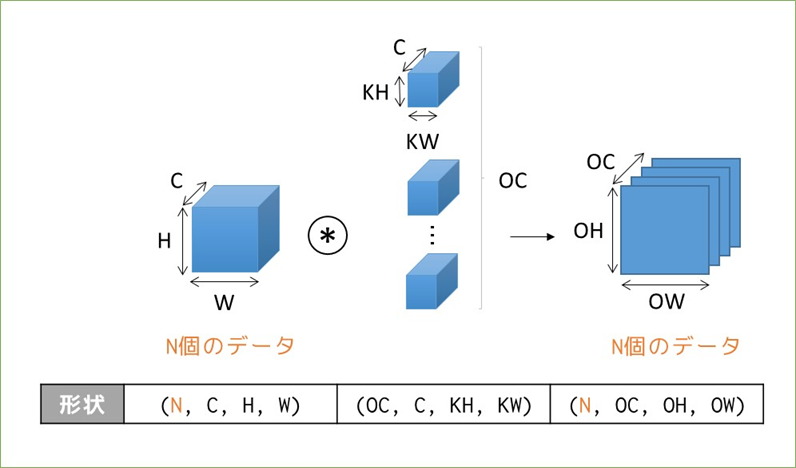
f:id:cha_kabu:20201123211825p:plain

表現の順番としては（バッチサイズ, チャンネル数, 高さ, 幅）の順で、フィルタは毎回同じものが適用されるので「N個のデータ」という概念がない点がいっつもややこしいです。。

ステップ57 conv2d関数とpooling関数

いよいよ実装です。タイトルの関数の他、書籍で説明がないim2colもまとめていきたいと思います。

im2col関数

DeZeroのfunctions_convモジュールにある、Functionを継承したクラスです。クラスそのものよりもforward処理で呼び出しているim2col_array関数の理解が重要です。この関数が何をやっているかをざっくりと言うと「画像を（工夫して）行列に変換」しています。何でわざわざそんなことをするかというと、「その方がnumpyの計算効率が良いから」です。行列に変換される過程と、少し先取りして畳み込み演算が行われる様子も合わせて図にまとめていきます。

まずこれからやることの全体像です。※先ほどまでは書籍に則ってブロックで考えていましたが、以降は平面で考えることにします。ブロックで考えると概要は掴めるのですが、「実際に各値がどうなっているのか？」を掴むには平面で考えた方が良いと思います。

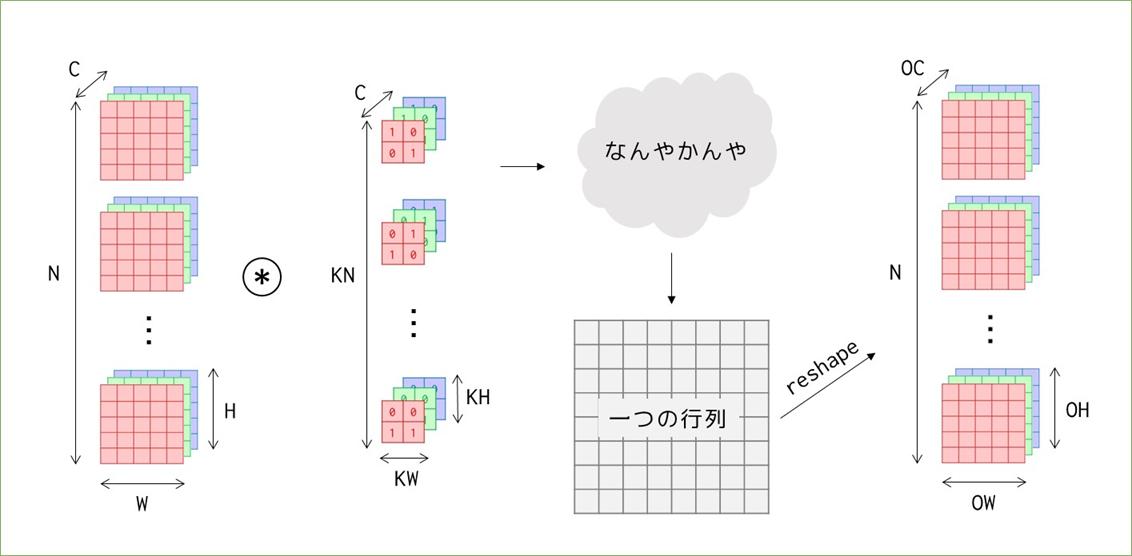
f:id:cha_kabu:20201123211838p:plain

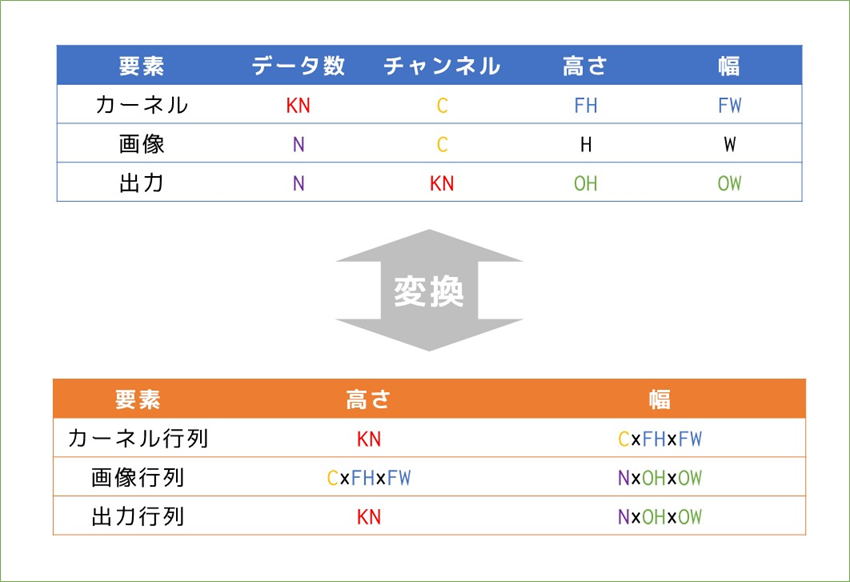
(N, C, W, H)の画像に、(KN, C, KW, KH)のカーネルを適用し最終的には特徴マップを出力に得ます。覚えておきたいのは、途中の「なんやかんや」の計算によって特徴マップの前（と、実は画像とカーネルの要素積を行う前）に、バッチ数やチャンネル数に関わらず一つの大きな行列が出来上がるということを覚えておいてください。

N=C=KN=1の場合：素朴なim2col

まずは簡単なパターンから、バッチサイズ1、チャンネル数1のグレー画像4×4に2×2のカーネルを適用することを考えます。im2colを考えない畳み込み演算は以下の様にカーネルと画像の該当箇所の要素積で出力が求められます。

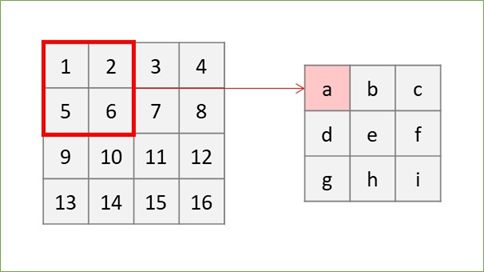
f:id:cha_kabu:20201123211854p:plain

この計算をどうやって行うかというと、無理くりfor文を繰り返すことでもできますが、その場合一か所辺りカーネルのマス数4回×9回移動＝36回のループ計算が必要になります¹。一方以下のように考えると行列積で考えられ、計算量を削減できます。

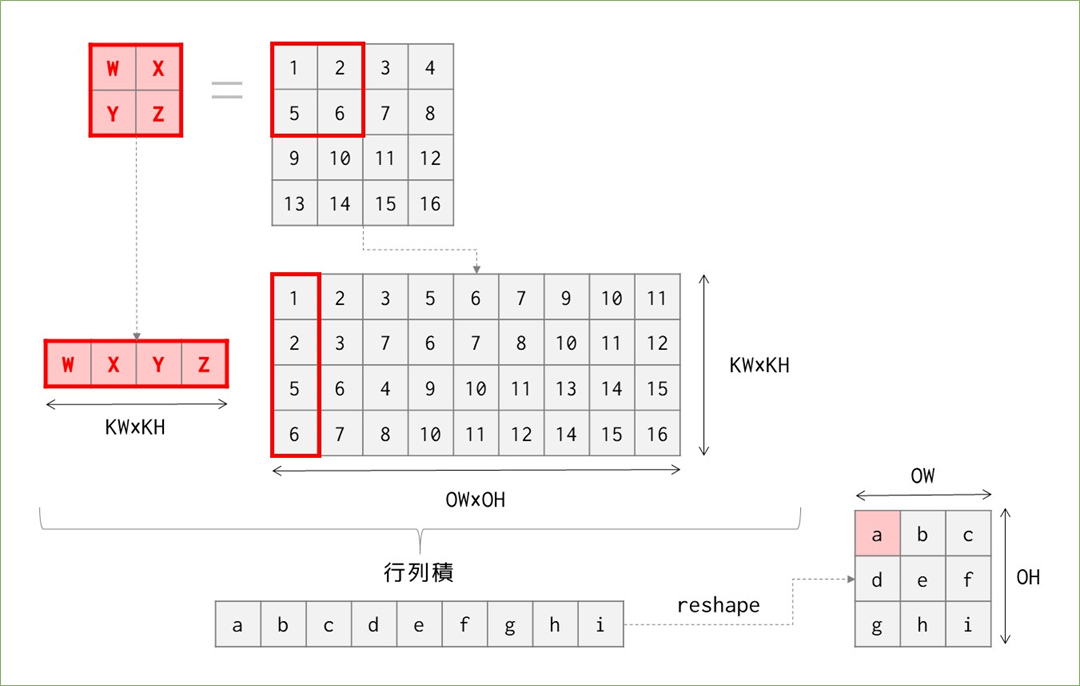
f:id:cha_kabu:20201123211907p:plain

図の4*4の画像を4*9に変換しているところが素朴版im2colがやっていることです。これにより、計算量は"ほぼ"（実際にはカーネルの変換、行列積、reshapeで各1回必要なので"ほぼ"です）画像の変換回数（カーネルが動く回数）分で済むので、36回→9回に納めることができました。以上、im2colの説明！…とはならず、改善が考えられます。

N=C=KN=1の場合：改良版im2col

結論を先に言うと、先ほどまでの計算方法では計算量は出力の要素分だけ必要だったのに対し、これから行う方法では出力のサイズに関わらず、カーネルの要素数分だけのループ計算で済みます。イメージとしては、先ほどの図では画像の変換をカーネルを1マスずつ動かして縦に並べることを繰り返していたところ、今度は出力のサイズのマスを動かしながら横に並べていきます。

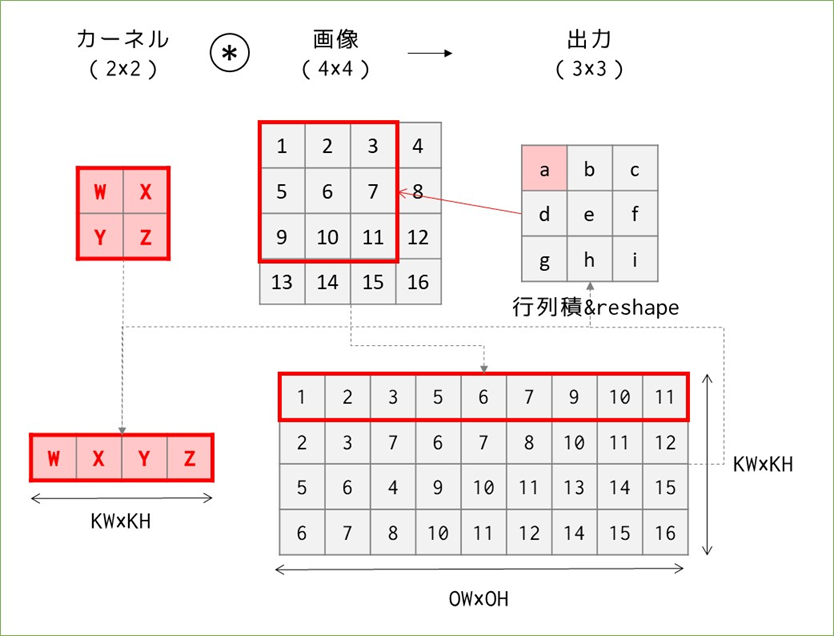
f:id:cha_kabu:20201123211924p:plain

図にすると↑の様な形で、先ほどまでと違って出力のサイズを先に見て、同サイズのカーネル"もどき"を画像の中で動かして要素を横に並べます。これでも変換後の行列は先ほどと同じものになっているので、後は先ほど同様にカーネルを横に並べたものとの行列積を求めてreshapeすると出力を得ることができます。行列積とreshapeを除けば、計算量は36→9→4回まで減りました。

この改良の凄いところは、計算量がKW×KH=カーネルの要素数で済むということで、元の画像のサイズに関係なく計算量を一定に保てます。※パディングやストライドは無視した話です。

N,C,KN > 1の場合：素朴なim2col

続いてバッチ処理とRGB画像を扱う場合を考えます。まずはim2colを使わずに、畳み込みだけを考える場合です。

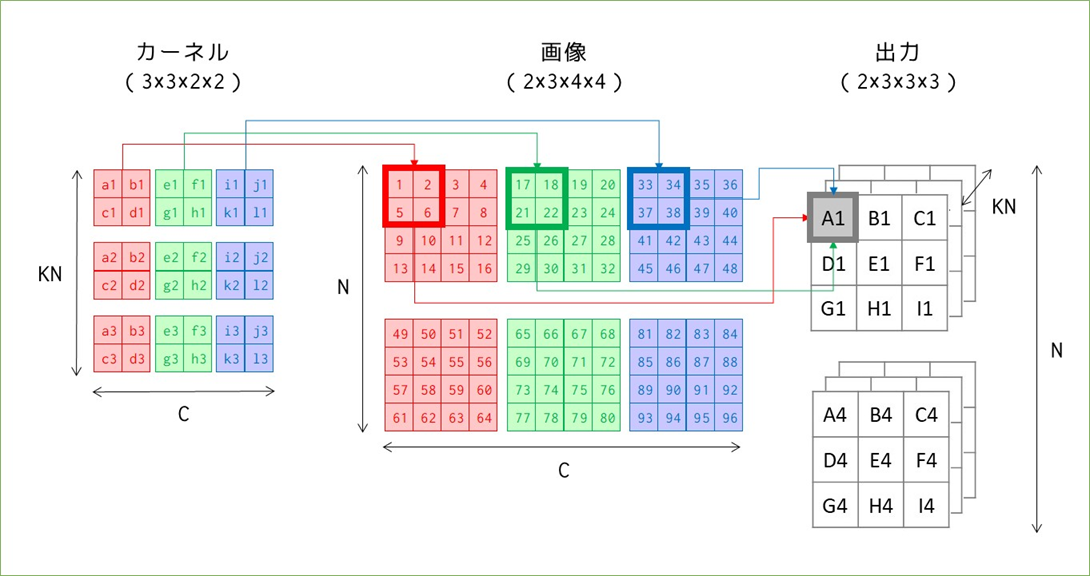
f:id:cha_kabu:20201123211941p:plain

変化があったところだけ記号を付けています。カーネルと画像は同じチャンネル数3を持っており、これは出力のサイズに影響を与えていません。ただし、出力の1マスの計算が1カーネルマス分の積の和だったのに対し、3チャンネル分のカーネルマス分の積の和になっています（A1で例示）。

カーネル数KNは、出力のチャンネル数と対応しています。出力のチャンネル数はカーネルと画像のチャンネル数ではなく、カーネル数に左右されるというのが少し分かりにくいです。図では表せていませんが、A1~I1の出力の後ろにはA2~I2の出力が並んでおり、その計算は2つ目のカーネルと1つ目の画像で行われます。

画像のバッチサイズNは出力のデータ数と一致します。2つ目の画像49～96と3つのカーネルすべてを使って2つ目の出力を得ます。

この計算量は合っている自信はありませんが…最初のグレーチャンネルの36回をベースに、3チャンネル分×2バッチ分の6倍必要なので、216回のループ処理が必要になります。²

これも先ほどの例と同様にim2colを使うと行列演算をすることができます。

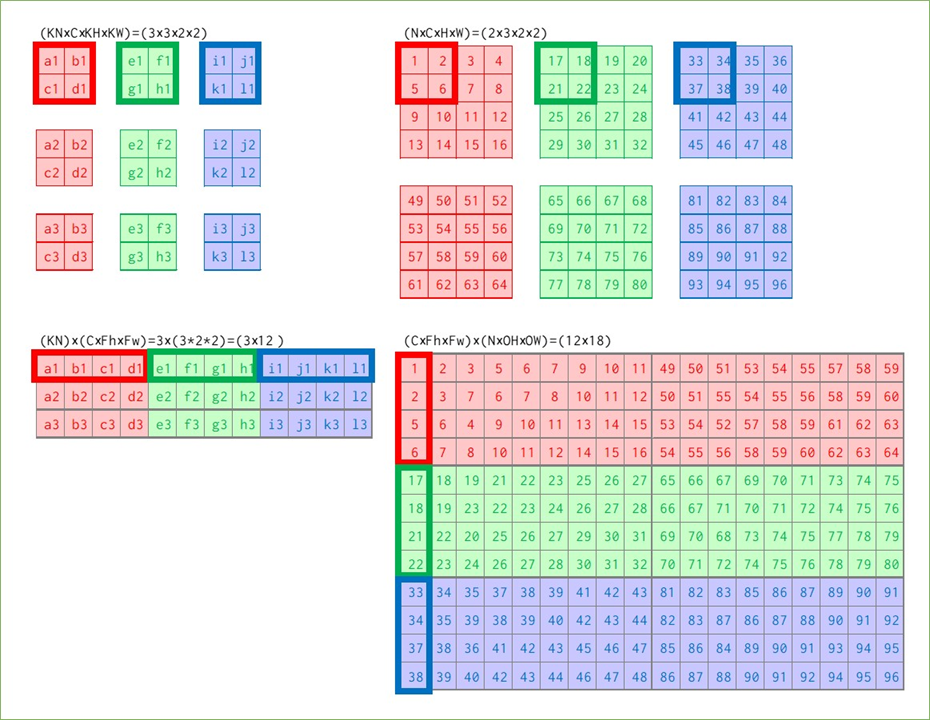
f:id:cha_kabu:20201123211955p:plain

細かすぎて見えない＆スペースの問題で出力を省略していますが…行列の並べ方に注意してください。カーネルは横にチャンネル、縦に種類を並べており、画像は横に種類、縦にチャンネルを並べています。小さく各サイズを書いていますが、カーネルは(3×12)、画像は(12×18)の行列となり、(3×18)の出力（reshape前）を得ます。先ほど単純な畳み込みで見たときの出力の総マス数は9*3*2=54マスで、今回は3*18=54マスなので、reshapeすれば同じ出力を得られることが想像できます。

この場合の計算量は、ほぼカーネルと画像の変換回数だと考えると、カーネルは単純に9個を横に並べるだけなので9回、画像は1つあたり9回の移動がありそれが6個あるので9*6=54回で合計9+54=63回のループで計算できます。216回よりかはだいぶ少なくなりましたが、先ほどと同様の方法で削減できます。

N,C,KN > 1の場合：改良版im2col

小見出しが嘘になってしまうのですが、効率的に並べる方法は1チャンネルの時と同じなので省略します。計算量としてはカーネルのマス数＝4マス/個でカーネルが全部で9個あるので36回の計算で済みます。

改良版だけではなく素朴版も同じですが先ほど画像に入りきらなかった出力への変換を見てみます。

f:id:cha_kabu:20201123212006p:plain

先ほど説明した通り、(3×12)のカーネル行列と(12×18)の画像行列の行列積をとると(3×18)の出力行列ができ、それをreshapeして出力（2×3×3×3）を得ます。

im2colまとめ

これまで見てきたことをアルゴリズムとして実装するためのim2col関数の中身は、素人には厳しいコードとなっています…。しかし「使う」という観点ではこれまで見てきた様に各要素のサイズがどう変換されているか、何が対応しているかを覚えておくことの方が重要かと思うので、最後にそれをまとめてim2colは終わりにしておきます。そしてここまで書いて気付いたのですが書籍の実装や説明に対して高さと幅すべて転置の状態で説明していましたね…しかし説明を修正するのも面倒なのでこのままいきます。。形が転置（高さと幅が入れ替わる＆行列積の際に画像とカーネルの位置関係が変わる）になるだけでやっていることは同じです！

f:id:cha_kabu:20201123212019p:plain

im2colと畳み込み演算によって、カーネルと画像が行列に変換され出力を行列で得て、それをreshape(はたまたcol2im）によって再度変換して最終出力を得ます。

また、ここまでストライド1固定でパディングのことは考えずにやってきましたが、長くなってしまったのとそれらもim2colを使う際にはパラメータ設定だけで意識せずで良さそうなので先に進みます…

conv2d関数

行われることはim2colと一緒に説明しました。書籍で紹介されているconv2d_simple関数についてはカーネルをreshapeしたりtransposeしたりしていますが、先ほど説明したことの実装です。関数の中身を分解して使って、先ほどの具体例と同じ結果になるかだけ見てみます。

先に補足しますと、先ほど説明した具体例と形状を合わせるため、一部書籍とコードが異なります。また、出力行列を正しく出力に戻せているか確認するためカーネルの重みは3個それぞれ0.1,0.2,0.3として、事前にExcelで計算した結果とあっているか確認します。

import numpy as np
import dezero.functions as F

# 入力（画像ダミー）の作成：(N×C×H×W)=(2×3×4×4)
x = np.arange(1,97).reshape(2,3,4,4)

# カーネル（重み）の作成：(KN×C×KH×KW)=(3×3×2×2)
w1, w2, w3 = np.full((3,2,2),0.1), np.full((3,2,2),0.2), np.full((3,2,2),0.3)
W = np.array([w1,w2,w3])
print(W.shape) #(3, 3, 2, 2)

# 入力にim2colを適用→書籍と逆に説明していたので転置
col = F.im2col(x,(2,2)).transpose()
print(col.shape) # (12, 18)

# カーネルはreshapeで変形→書籍と逆に説明していたので転置しない
W = W.reshape(3,-1)
print(W.shape) # (3, 12)

# 行列積（linear関数を適用）で出力行列を求める
t = F.linear(W, col, b=None)
print(t.shape) # (3, 18)

# 出力の形にreshape：(N×KN×OH×OW)
t.T.reshape(2,3,3,3).transpose(0,3,1,2)

結果の数字に意味は無いので省略しますが、事前の計算結果と一致しました。

続いて書籍ではConv2dレイヤを実装しますが、やっているのは__init__()で主にconv2d_simple関数に渡すインスタンス変数を宣言、_init_W()で初回のカーネルの重みを初期化し、forward()では初回は_init_W()を呼び出しあとはconv2d_simple関数を呼び出して出力を返すだけです。

pooling関数

maxプーリングを行う関数の実行です。実施内容は全く異なりますがコードとしてはconv2d_simple関数と似通っている（出力にim2colを適用して行列化→reshape→行方向に最大値を求める→reshapeして出力）のでここまでを理解できていれば特に難しくないと思います。

代表的なCNN（VGG16）

VGG16クラスの実装については画像処理を行ったことがあれば意味は分かると思います。ここでは各処理を行ったときのサイズを確認しておきたいと思います。入力画像のサイズは(10, 3, 224, 224)を仮定しています。

__init__()	forward()	サイズ
self.conv1_1 = L.Conv2d(64, kernel_size=3, stride=1, pad=1)	x = F.relu(self.conv1_1(x))	(10, 64, 224, 224)
self.conv1_2 = L.Conv2d(64, kernel_size=3, stride=1, pad=1)	x = F.relu(self.conv1_2(x))	(10, 64, 224, 224)
	x = F.pooling(x, 2, 2)	(10, 64, 112, 112)
self.conv2_1 = L.Conv2d(128, kernel_size=3, stride=1, pad=1)	x = F.relu(self.conv2_1(x))	(10, 128, 112, 112)
self.conv2_2 = L.Conv2d(128, kernel_size=3, stride=1, pad=1)	x = F.relu(self.conv2_2(x))	(10, 128, 112, 112)
	x = F.pooling(x, 2, 2)	(10, 128, 56, 56)
self.conv3_1 = L.Conv2d(256, kernel_size=3, stride=1, pad=1)	x = F.relu(self.conv3_1(x))	(10, 256, 56, 56)
self.conv3_2 = L.Conv2d(256, kernel_size=3, stride=1, pad=1)	x = F.relu(self.conv3_2(x))	(10, 256, 56, 56)
self.conv3_3 = L.Conv2d(256, kernel_size=3, stride=1, pad=1)	x = F.relu(self.conv3_3(x))	(10, 256, 56, 56)
	x = F.pooling(x, 2, 2)	(10, 256, 28, 28)
self.conv4_1 = L.Conv2d(512, kernel_size=3, stride=1, pad=1)	x = F.relu(self.conv4_1(x))	(10, 512, 28, 28)
self.conv4_2 = L.Conv2d(512, kernel_size=3, stride=1, pad=1)	x = F.relu(self.conv4_2(x))	(10, 512, 28, 28)
self.conv4_3 = L.Conv2d(512, kernel_size=3, stride=1, pad=1)	x = F.relu(self.conv4_3(x))	(10, 512, 28, 28)
	x = F.pooling(x, 2, 2)	(10, 512, 14, 14)
self.conv5_1 = L.Conv2d(512, kernel_size=3, stride=1, pad=1)	x = F.relu(self.conv5_1(x))	(10, 512, 14, 14)
self.conv5_2 = L.Conv2d(512, kernel_size=3, stride=1, pad=1)	x = F.relu(self.conv5_2(x))	(10, 512, 14, 14)
self.conv5_3 = L.Conv2d(512, kernel_size=3, stride=1, pad=1)	x = F.relu(self.conv5_3(x))	(10, 512, 14, 14)
	x = F.pooling(x, 2, 2)	(10, 512, 7, 7)
	x = F.reshape(x, (x.shape[0], -1))	(10,25088)
self.fc6 = L.Linear(4096)	x = F.dropout(F.relu(self.fc6(x)))	(10,4096)
self.fc7 = L.Linear(4096)	x = F.dropout(F.relu(self.fc7(x)))	(10,4096)
self.fc8 = L.Linear(1000)	x = self.fc8(x)	(10,1000)

基本的なことですが、以下の様にサイズが変化しています。

Conv2dレイヤを通るとチャネル数が変化する（かそのまま）
pooling関数を通すとHとWが半分になる
reshapeでNを保持して行列に変換する：サイズが（N, C×H×W）になる
全結合層を通して行列のサイズを（10, 4096）に小さくして
最後に（N, 1000）にする。1,000は学習済みモデルの分類数なので、学習済みモデルを使用しない場合は適宜変更する。

以降の使い方はお作法的なものはありますが内容は難しくないかと思います。

最後に

おそらく次で最後！何とか初期に考えていた1か月で読破できそうです。

要素積で求めれば9回で済む気もしますが話の流れ的にそんなものは無いこととします。どちらにせよ以降の改善はした方が良いので気にしない。↩
最初の例同様に、要素積を使えば計算量は4分の1に抑えられる気がしますが…先ほどと同様の理由でそんなものはないこととします。↩

2020-11-22

ゼロから作るDeep Learning3　フレームワーク編を読む　その⑪ステップ52～54

はじめに

以下の記事シリーズの続きです。

cha-kabu.hatenablog.com

本編

ステップ52 GPU対応

このステップは…スルーします！他ライブラリ使う時はお決まりのお作法（GPU使用可能確認してオブジェクトをGPUに投げる）をしておけばとりあえずできますし、自分のPCが2012年頃？に買ったやつで、当時動画編集もしてたのでNVIDIAのQuadro K600っていう確か当時はそれなりだったGPUが載ってるのですがこいつがどこまでやれるのかも分からないし、何よりそもそも自分の環境でcupyを使えるようにできませんでした…

こちらのサイト様を参考にCUDAもCuPyもインストールはできたのですが、いざimport cupyとすると、

'CUDA path could not be detected.'

と言われてしまい…全然意味は分かっていませんが環境変数PATHとやらもちゃんと設定されているんですけどね…軽く数日かかりそうなのでスルー！

それはそうと参考先サイトの充実度がすごい…設定関係がすべて図付でめちゃくちゃ分かりやすい…

ステップ53 モデルの保存と読み込み

コード自体は難しくないと思いますが、書籍の具体例で何が起こっているかを見てみます。まず、modelの構造とsave_weights()内で_fratten_params()メソッドがどのようなことを行っているかまとめます。

f:id:cha_kabu:20201122210057p:plain

Layer（あるいはそれを継承した）インスタンスで_fratten_params()メソッドが実行されると、空の辞書にParameterインスタンスの値（Parameter.data）をParameterが存在する階層に関わらずすべて格納します。その時、辞書のkeyはParameter自身の名前と親のLayerの名前を"/"で繋げたものになります。

そうしてできた辞書に格納されている値はVariableでnumpyでは保存ができませんので、図では省略しましたがarray_dictというndarrayで値をもった別の辞書を作成し、それをnp.savez_compressed関数で保存します。

そして、load_weights()メソッドを新しく作成したModelインスタンス（各パラメータの値は初期化されてしまっているが、構造は保存したものと同じ）で呼び出すと、対応するkeyのデータを各パラメータに設定してくれます。

注意というほどでもありませんが、保存しているのは例えばmodel.l0.W.dataの値だけですので、これ以外の情報は読み込まれません。具体例として、modelで学習したパラメータを保存しておき（コードは省略）、model2に読み込んで各インスタンス変数を確認すると以下の様になっています。

# modelのインスタンス変数確認
print(model.l1.b.data) # [-0.00109223  0.00141618 -0.00185522 ...]
print(model.l1.b.grad) # variable([-0.01123966 -0.01110208  0.01427339 ...])

# 同じ構造のモデルをmodel2として作成、modelのパラメータ値をロード
model2 = MLP((1000, 10))
model2.load_weights("array.npz")

# model2のインスタンス変数確認
print(model2.l1.b.data) # [-0.00109223  0.00141618 -0.00185522 ...]
print(model2.l1.b.grad) # None

ステップ54 Dropoutとテストモード

なんだか…突然説明が雑では…書いてあることは分かるので先に進もうかと思いますが、DeZeroでどうやってDropout実装するのかの説明が今までと比べて急にあっさりで…関数としての実装なので、コンストラクタでは何もせずに活性化関数の様にforwardメソッドに書けば良いのでしょうか…？一応↓のクラスを作ったところ、動きはしました（正しい自信はないです…）。

class ThreeLayerNet(Model):
    def __init__(self, hidden_size, out_size):
        super().__init__()
        self.l1 = L.Linear(hidden_size)
        self.l2 = L.Linear(hidden_size)
        self.l3 = L.Linear(out_size)

    def forward(self, x):
        y = F.dropout(self.l1(x))
        y = F.relu(y)
        y = F.dropout(self.l2(y))
        y = F.relu(y)
        y = self.l3(y)
        return y

最後に

めちゃくちゃ短いですが先に進むとキリが悪いのでここまで！残すはCNNとRNN（+LSTM）です。書籍の説明はあっさりしていそう＆今まで雰囲気で写経してしか使ってないので長くなりそうです…次回は～ステップ58を予定。

2020-11-22

ゼロから作るDeep Learning3　フレームワーク編を読む　その⑩ステップ49～51

はじめに

こちらの記事シリーズの続きです。

cha-kabu.hatenablog.com

本編

ステップ49 Datasetクラスと前処理

他のライブラリはあまり詳しくありませんが、PytorchではおなじみのDatasetクラスを定義します。カスタムデータセットを作成するときに継承するやつですね。書籍では（今のところ）datasetsモジュールに用意されたデータしか用いないのでコンペ等で使う時と少しお作法が異なりますが、あまり意識せずに写経しながら利用していた__getitem__()と__len__()の二つの意味がやっとわかりました。前のステップとの変化で見てみます。

# ステップ48
x,t = dezero.datasets.get_spiral(train=True)
print(x[0],t[0]) # [-0.13981389 -0.00721657] 1
print(len(x)) # 300

# ステップ49
train_set = dezero.datasets.Spiral(train=True)
print(train_set[0]) # (array([-0.13981389, -0.00721657], dtype=float32), 1)
print(len(train_set)) # 300

以下の様な違いが分かります。

命令	ステップ48	ステップ49
教師データとラベルデータの取得	別々（x,t）	セット（train_set）
インデックスを指定したとき	各データを取得 or 各データをタプルにまとめて取得	各データの組をタプルで取得 ※クラス次第で、100%ではない
len()を使用したとき	各データの長さを返す	設定により、self.dataの長さを返す

__getitem__()はDataset（を継承した）インスタンスをndarrayみたいにインデックス指定で中身のデータを覗けるように指定し、__len__()も似たように長さの概念がないインスタンスでも普通のデータの様に長さを返せるようにlen関数が使われたときはlen(train_set.data)を返す様にクラスを定義します。

…とまぁ違いは分かったのですが、書籍で説明がある、

Datasetクラスを使う利点は、別のデータセットで学習を行う時に実感できます。

についてはこれまでコピペ＆写経でしか使ってこなかったからか余り実感がないですね。。コードの短さ的にも（Dataloaderやtransformなどを無視すると）直接取得したほうが手っ取り早い気がしますし、例として提示されているBigDataクラスでは各データをタプルで返さずに別個で返していてそこは統一する必要はなさそうだったり、いまいちどこが肝なのかがまだ分かりません…とりあえず中身については分かったので先に進みます。

それともう一つ未だに分かっていないのがDataset（を継承した）クラスをインスタンス化した際、インスタンス変数のデータはどこに保存されているのかということです。BigDataクラスの説明で以下の文章があります。

BigDataクラスの初期化時にはそれらのデータの読み込みは行わずに、データへアクセスがあったタイミングで読み込むようにします。

ということで__getitem__()内でnp.load()が使用されていて、それ自体は分かるのですが、ここで先ほどインスタンス化したtrain_setとget_spiral()で取得したxの容量を見てみます。

import sys
print(sys.getsizeof(train_set)) # 56
print(sys.getsizeof(train_set.data)) # 2512
print(sys.getsizeof(x)) # 2512

インスタンス変数に格納したデータって、インスタンス自身が持っているのだと思っていたのですが違うのですね。しかしオブジェクトの一覧を出してみてもtrain_set.dataは出てこず…いったいどこでどんな形で保存されているんでしょう？この辺の知識は全然ないので何を調べていいのかすら分かっていません。。

ステップの後半ではtransform機能を実装するのですが、肝心のtransformsモジュール内の各クラスに関する説明が随分とあっさりしているので簡単にまとめます。まずはコードを見れば分かることですが基本的な使い方をしたときに何が起こっているのかのフローから。

f:id:cha_kabu:20201122074458p:plain

transformsモジュールを使うことが必須なわけでなければ、Composeクラスを使う必要もないのですが、とにかく行いたい処理を実装したものをインスタンス化したり、関数化します。それをDataset（を継承した）クラスをインスタンス化する際に引数transformsに与えてやると、__getitem__()でデータを返す時にデータをそのインスタンスや関数に通したものを返してくれます。

さて、突然出てきたComposeが何者かということでコードを見てみます。

class Compose:
    """Compose several transforms.
    Args:
        transforms (list): list of transforms
    """
    def __init__(self, transforms=[]):
        self.transforms = transforms

    def __call__(self, img):
        if not self.transforms:
            return img
        for t in self.transforms:
            img = t(img)
        return img

注記にもありますが、インスタンス化時の引数にはtransforms（変換処理）をリストで受け取ります。そしてDataset（を継承した）クラスの__getitem__()内でインスタンスに入力が与えられると、__call__()によって自動的に呼び出される処理で、transformsがNoneでなければ各処理を順に適用したうえで返します。

Composeの引数に入れるtransformsにどんなものがあるかはたくさんあるので省きますが、最低限「transformsモジュールのComposeクラスに、同じくtransformsモジュールの他の変換処理を行うクラスをリストで渡してインスタンス化する」というお作法を覚えておけば、混乱することは無いかと思います。※リストで渡すのは必ずしもtransformモジュールのものでなくとも、自作の関数などでも問題ないです。

ステップ50 ミニバッチを取り出すDataLoader

こちらもpytorchではおなじみDataLoaderです。イテレーターなど細かいところを深掘るとちょっとややこしい気もしますが、流れを理解するだけであればそう難しくありません。DataLoderクラスの有無でコードがどう変わったかだけメモしておきます（accuracy算出の追加など、関係のない修正は無視）。コメントアウトしている部分が以前の実装で、DataLoderクラス内で処理が行われています。

max_epoch = 300
batch_size = 30
hidden_size = 10
lr = 1.0

train_set = dezero.datasets.Spiral(train=True)
test_set = dezero.datasets.Spiral(train=False)
############################# 追加 #############################
train_loader = DataLoader(train_set, batch_size)
test_loader = DataLoader(test_set, batch_size, shuffle=False)
################################################################

model = MLP((hidden_size, 10))
optimizer = optimizers.SGD(lr).setup(model)

# data_size = len(x)
# max_iter = math.ceil(data_size / batch_size)

for epoch in range(max_epoch):
    # データセットのインデックスのシャッフル
    # index = np.random.permutation(data_size)
    sum_loss, sum_acc = 0,0
    
    # for i in range(max_iter):
    for x, t in train_loader:
    # ミニバッチの作成
    # batch_index = index[i * batch_size:(i + 1) * batch_size]
    # batch = [train_set[i] for i in batch_index]
    # batch_x = np.array([example[0] for example in batch])
    # batch_t = np.array([example[1] for example in batch])
        
        y = model(x)
        loss = F.softmax_cross_entropy(y, t)
        acc = F.accuracy(y, t)
        model.cleargrads()
        loss.backward()
        optimizer.update()
        
        sum_loss += float(loss.data) * len(t)
        sum_acc += float(acc.data) * len(t)
    
    print("epoch:{}".format(epoch+1))
    print("train loss: {:.4f}, accuracy: {:.4f}".format(
        sum_loss / len(train_set), sum_acc / len(train_set)))

ステップ51 MNISTの学習

他でDeepLearningを学んだ人ならみんな通る道MNISTです。特に新しいこともないのでまとめるものはありませんが、これまでの積み重ねでコードがめちゃくちゃ分かる様になりました…！特にデータセット作成のところは今まではソースコードを見ることもしていなかったので「この引数なんなの？？？」と思っていたのですが、とてもクリアになりました。。

最後に

やっと第4ステージ終了です！次からラストステージへ！次回は～ステップ54を予定。

2020-11-22

ゼロから作るDeep Learning3　フレームワーク編を読む　その⑨ステップ46～48

はじめに

以下のシリーズ記事の続きです。

cha-kabu.hatenablog.com

本編

ステップ46 Optimizerによるパラメター更新

最適化手法の基底クラスとなるOptimizerクラスを作成し、それを継承してSGDとMomentumを実装します。

基底クラスのOptimizerクラスの実装はメソッドは多いですが一つ一つがやっていることは単純です。分からなかったのは何故わざわざsetupメソッドでtargetとするModelクラスもしくはLayerクラスを指定するのでしょう？継承先のクラスで引数に与えてやれば良い気もするのですが…pytorchを使っているときはこのsetupメソッドに該当する記述は不要¹なので必要性が分からなかったのですが、何か理由あってのことだと思うのでひとまず書籍に従います。参考までに、以下のコードでも動きました。

class SGD(Optimizer):
    def __init__(self, target, lr=0.01): 
        super().__init__()
        self.lr = lr
        self.target = target # オリジナルの実装 
        
    def update_one(self, param):
        param.data -= self.lr * param.grad.data

##### 省略 #####

model = MLP((hidden_size, 1))
optimizer = optimizers.SGD(model,lr) # 書籍ではoptimizers.SGD(lr).setup(model)

##### 省略 #####

また、add_hookメソッドの説明がだいぶあっさりしています（このあとのステップで使うのかも知れません）が、パラメータ更新前に前処理を行う関数を追加するメソッドとのこと。公開されているoptimizerモジュールには以下の三つが実装されています。

WeightDecay

日本語だと重み減衰って言うんですね。過学習対策に使われるもので、損失関数に正則化項（DeZeroではL2ノルム）を加えます。具体的には、損失関数が $\displaystyle{L(\Theta)}$ から以下の形に変化します。※ $\displaystyle{\Theta}$ は「すべてのパラメータ」

$\displaystyle{L(\Theta)+\lambda\dfrac{1}{2}\sum_{w}||w||^{2}}$

$\displaystyle{\lambda}$ はハイパーパラメータでこの値が大きいほど大きな重みをとることにペナルティを与えることになります（≒パラメータが少しずつしか変化しない）。損失関数が変化したことにより、逆伝播する勾配の値も右辺部分を微分した形が残ることになり、以下の様に変化します。

$\displaystyle{ w \leftarrow w-\eta \left(\dfrac{\partial L(\Theta)}{\partial w} + \lambda w\right)}$

WeightDecayはDezeroでは以下の様に使用することができます。ハイパーパラメター $\displaystyle{\lambda}$ は以下の例の様に、他コンペを見ていても $\displaystyle{1e-3}$ よりは小さい程度の値が設定されていることが多い気がします。

optimizer.add_hook(dezero.optimizers.WeightDecay(1e-4))

ClipGrad

いわゆる「勾配爆発」を食い止めるための機能。取り得る勾配の上限値を指定して、それを超えた場合に上限値で正規化します。具体的には上限値 $\displaystyle{M}$ 、勾配を $\displaystyle{g}$ とすると、以下の様にします。

$\displaystyle{g = \dfrac{M}{||g||}g}$

FreezeParam

確証が持てなかったのですが恐らく転移学習をするときによく使うフリーズの機能ですかね？中身は単純で、引数に可変長でLayerクラスを受け取り、パラメターのgradをNoneにします。試していないのですがloss.backward()とoptimizer.update()の間で呼び出して使う感じでしょうか？

こちらはいったん寝かして置き、後半のステップでVGG16の実装があるのでそちらで確認したいと思います。

続いてSGDクラスの実装がされているのですが、まだミニバッチの機能を実装していないので、挙げられている使用例は確率的勾配降下法とは言えず通常の勾配降下法ですよね…？

最後に、SGD以外の最適化手法の実装紹介としてMomenumSGDが紹介されています。コードの見た目は簡単ですが、何を更新しているのかが追わないとパッと理解できなかったのでメモしておきます。

f:id:cha_kabu:20201121232614p:plain

大元はModelインスタンスですが、実際はその中身のParameterインスタンスを追っていくことになります。上図の通りなのですが敢えて言葉で説明すると…

Modelクラスをインスタンス化したmodelをtargetとしてそのインスタンス変数_paramsの中身を確認 → l0,l1の取得
model._paramsに保存されていたLinearインスタンスのインスタンス変数の_paramsの中身を確認 → l0,l1それぞれのW,bを取得
2で確認した各層のパラメータを格納しているParameterインスタンスのオブジェクトidと、そのdataと同じ形状のゼロ行列をディクショナリのインスタンス変数self.vsに格納
2で確認した各層各パラメータの勾配の値を使ってパラメータ自体の値を更新する

…入れ子構造が分けわからなくなりますね。。書籍上は以上ですが、最適化手法の数学的性質、雰囲気だけで流してきたのでいつか別記事でまとめたいと思います。

ステップ47 ソフトマックス関数と交差エントロピー誤差

タイトル通りソフトマックス関数と交差エントロピー誤差を実装します。事前知識あったので特に分かりづらい点はありませんでしたが、数式がすらすら書けるほどは頭に入っていないので一応まとめておきます。

ソフトマックス関数

分類問題の出力層で使われることが多い活性化関数（と言ってよいのか？）です。出力の数値を確率に変換してくれます。数式は以下の通りで、分子は入力の指数関数、分母はすべての入力の指数関数の和。

$\displaystyle{ p_{k} = \dfrac{exp(y_{k})}{\sum_{i=1}^{n}exp(y_{i})} }$

交差エントロピー誤差

多値分類問題で使われる損失関数、別名logloss。低い方が良く、完全ランダムな時は以下の計算式から0.693になります。ごつい数式をしていますが、要するに「正解している予測の予測確率のlogをとり合計してマイナスを掛けている」だけです。

$\displaystyle{ L=-\dfrac{1}{N}\Sigma_{i=1}^{N}(y_{i}\log p_{i}+(1-y_{i})\log (1-p_{i}))=-\dfrac{1}{N}\Sigma_{i=1}^{N}\log p'_{i} }$

$\displaystyle{y_{i}}$ は正例かどうかを表すラベルで、 $\displaystyle{p_{i}}$ は各レコードが正例である予測確率。 $\displaystyle{p'_{i}}$ は真の値を予測している確率。正解が $\displaystyle{1}$ の時は $\displaystyle{\log p_{i}}$ を掛けて、正解が $\displaystyle{0}$ の時は $\displaystyle{\log (1-p_{i})}$ を掛けたものの総計をとって $\displaystyle{-\frac{1}{N}}$ 倍しています。

突然出てきた「エントロピー」という謎の言葉や、何故対数をとるのか等についてはこちらのサイト様の説明が分かりやすいです。※交差エントロピー誤差についての説明ページではありません。

また、これらの関数は書籍上はpythonの関数を作成する方法defで作成されていますが、ライブラリではFunctionを継承したクラスで実装されています。クラスでは他の関数同様にforwardメソッドで関数的な計算が、backwardメソッドでは逆伝播が行われ値を返します。ソフトマックス関数と交差エントロピー誤差の逆伝播についてはゼロから作るDeepLearning①の巻末付録Aが詳しいです。

ステップ48 多値分類

オリジナルの3値分類を行います。この後DataLoderの実装などがありますが、DeepLearningの学習の流れ全体が分かりやすいのはここだと思うのと、いつもなんとなく写経してしまって分かった気になっているので、学習のループがどう回っているのか視覚的に捉えられる様に表にしました。※コード例のところは一部あまりよろしくない簡素化を行っています。

f:id:cha_kabu:20201121232636p:plain

表の例も他で良く見る形に変えてしまったのですが、書籍の以下のコードは見慣れなくて少し戸惑いました。

sum_loss += float(loss.data) * len(batch_t)

lossの合計に1ループ分のlossを加算する際、バッチデータの長さを掛けています。そしてそのあとループの外では

avg_loss = sum_loss / data_size

lossの合計をデータサイズで割って平均としています。よく見るのは、lossの合計は単純な1ループ分の合計（バッチデータの長さを掛けない）で、そのあとバッチサイズで割るパターンだと思いますが、こちらはバッチ分割時に余りがでる際に対応した形式なのかと思います。確かにこちらの方が正確な平均lossが出せますね。

最後に

さっとまとめて進んでしまいましたが、最適化アルゴリズムと損失関数の数学的な側面はいっつも雰囲気だけで掴んでしまってたぶん良く分かっていないので、いつかちゃんと別記事でまとめる宣言をしてプレッシャーを自分にかけておきます。次回は～ステップ51を予定。

pytorchでは引数にparamsを渡すので修正版のコードの様に引数にModel（もしくはLayer）クラスを渡すのもそもそものお作法とも違うのですが。↩

2020-11-19

ゼロから作るDeep Learning3　フレームワーク編を読む　その⑧ステップ42～45

はじめに

以下のシリーズ記事の続きです。

cha-kabu.hatenablog.com

本編

ステップ42 線形回帰の理論

ここまでのステップの内容理解＆線形回帰について知っていれば難しくありません。全体の計算グラフは以下の様な形です。

f:id:cha_kabu:20201119154131p:plain

$x$ や $y$ も計算グラフの一員ですが、値を変化させたいのは $W,b$ だけですので、これまでの例と違い全てのノードのgradには興味が無く、 $W,b$ についてのみ興味があります。そんなわけで、loss.backward()ですべてのノードのgradはこれまで通り算出されるのですが、cleargrad()を行ったりdataを書き換えるのはこの二つだけになります。

ステップ43 ニューラルネットワークの実装

非線形なsin関数の予測のためにステップ42で使った線形回帰とシグモイド関数を使って2層のニューラルネットワークを作成します。こちらもニューラルネットワークに詳しければ難しくないと思います。ただ、自分は恥ずかしい話とても基本的なところを良く分かっていなかったと気づかされました…いよいよニューラルネットワークなので「良く見る例のネットワーク図を書いておこう！」と思ったのですが、あれ縦に列要素が並んでいるんですね…流石に分かってはいたのですが、図にしようとしてから「あれ？」となったので身についてはいなかったのだ思います。。戒めを込めてこの気付きを図にしておきます。

f:id:cha_kabu:20201119154142p:plain

改めて確認することでもないんですけどね…各層のノードは縦に並んでいるので頭の中で行を意味しているイメージがこびりついていました。

あとグラフ描画のためのコードが書籍GitHubに記載されているのですが、次元を合わせるために使用されているnp.newaxisを知らなかったので参考にしたサイトをメモ。

パラメータをまとめるレイヤ

いくつかプログラミング部分で知らないことがあったのでまとめておきます。

特殊メソッドsetattr

詳細はこちらのサイト様が分かりやすかったです。

まずそもそもこいつが何なのかですが、「インスタンス変数を設定するときに裏で呼び出されているメソッド」と考えておけば良さそうです。例えば以下のシンプルなクラスにインスタンス変数を設定し、それを変更することを考えます。

class Human():
    def __init__(self, age):
        self.age = age

# ①インスタンス化
human = Human(age=5)
print(human.age) # 5

# ②インスタンス変数の修正
human.age = 10
print(human.age) # 10

# ③インスタンス変数の修正（わざわざ__setattr__呼び出し）
human.__setattr__("age",20)
print(human.age) # 20

①でインスタンス化し、②でインスタンス変数ageにアクセスして修正する方法については通常良く行われることなので問題ないと思います。ですが、実は②の裏では③の様に__setattr__が呼び出されることでageの値が上書きされています。__setattr__の引数はコードの通りインスタンス変数名とそれに格納したい値です。図で表すと以下の様な関係です。

f:id:cha_kabu:20201119154156p:plain

上図の通常挙動で問題なければクラス内でわざわざ__setattr__メソッドを定義する必要はないのですが、特別な挙動を加えたいのであればオーバーライドして挙動を変えてあげます。書籍では以下の様にオーバーライドしています。

class Layer:
    def __init__(self):
        self._params = set()
    
    def __setattr__(self, name, value):
        # 変更点
        if isinstance(value, Parameter):
            self._params.add(name)
        # 通常の処理の呼び出し
        super().__setattr__(name, value)

変更点の通り、インスタンス変数を定義するときにその値valueがParameterのとき、インスタンス変数paramsにそのnameを渡します。その後は通常の処理を行います（通常処理も忘れずに書かないとparamsにnameを渡しただけで処理が終わってしまう）。これでLayerクラスはインスタンス変数を設定する際にそれがParameterインスタンスであれば_paramsにその変数名を格納する様になりました。

ここまでで未だによく分かっていないのが、Layerクラスは何も継承していないのにsuper()を使って誰を呼び出しているのでしょう…Layerクラス内では書き換えてしまっているので何かしら大本の処理を呼び出す必要があるのは分かるのですが、何を参照しているのかわかりませんでした…「すべてのクラスの親玉がいるんだろうな」ということにして先に進もうと思います。。

yield

Layerクラスの実装時に使用されています。初めて見たためこちらのサイト様で概要を掴みました。

クラスのまとめ

一つ一つの処理は難しいものではありませんが、Layerクラスの導入によって再び全体像が分かりづらくなってきましたので、改めて各クラスについてまとめておきたいと思います。まずは、どんなクラスがあるかからです。

f:id:cha_kabu:20201119154206p:plain

大きく分けると図の通り3つのクラスがあります。

VariableとParameter
この二つは兄弟の様な関係で、まったく同じ機能を持っています。なぜ同じ機能なのに分けているかというと、二つを区別するためです。Parameterはその名の通り「パラメーター」（値を変化させたい）を扱うクラスで、Layerクラスのインスタンス変数として機能し、学習時に値を更新していきます。そういう意味ではParameterの方が若干機能が多いのでお兄ちゃん的立ち位置かも知れません。 Variableは変数というよりも、「データ」などと認識したほうが良いかも知れません。Variableの値自体を更新することはほとんどなく、最初に渡した値を持ち続けます。ParameterはLayerクラスのインスタンス変数として使われるものでしたが、VariableはFuncitionのインスタンス変数にもなるし、入出力にもなります。パラメーター以外の大抵の数値が（意識してインスタンス化せずとも）Variableになります。
Function属
Functionを継承して作成される各クラスです。大きくわけてfunctionモジュールで定義されるものとcoreモジュールで定義されるものがあります。 coreモジュールで定義されるものはいわゆる「四則演算（+α）」で、基本的な計算を行います。ステップ20~22で演算子のオーバーロードを行っているので、あまりこれがクラスだと意識する必要はありません。 functionモジュールで定義されるのは「関数」です。関数といっても以下の様な色々な種類があります。
- Matmulやreshapeの様なプログラミング的な意味での「関数」
- 線形変換を行うlinear、活性化関数（ex.Sigmoid）、誤差関数（ex.MeanSquaredError）などの機械学習アルゴリズムの一部
coreモジュールも含め様々な種類がありますが、「計算グラフのどこかに存在する計算処理」という意味ではすべて同じ働きをするものです。
Layer属
Layerを継承して作成される、その名の通りDeepLearningの「層」を作るクラスです。Functionと似たようなコードが多くあるので親戚の様にも思えますが、イメージとしては「上司」の様な役割だと思います。Layerクラスの命令で（一部の）Functionが動き、Parameterが更新されるイメージです。

それぞれのクラスのネットワーク上での働きを、すべての働きはもう一枚絵にはできませんが書籍のLinear2層の例を使って図にしておきます。

f:id:cha_kabu:20201119154218p:plain

黒線が順伝播、赤線が逆伝播の動きです。

Linear層2つをインスタンス化、x（訓練データ）、y（教師データ）を用意しておく
- Linear層の中ではParameterも自動的にインスタンス化される
- xとyはVariableとしてインスタンス化しても良いが、計算処理時に自動的にVariableになるのでndarray形式でOK
predict関数を作成しておく　※Functionクラスの関数ではなく、いわゆる自作関数
以下処理をループしパラメータの更新を行う
1. predict関数にxを渡して実行
  1. xを引数に、Linear1の__call__メソッドが呼び出される→linearのforwardメソッドが実行される
  2. 1の結果を引数に、sigmoidを実行（内部で__call__メソッドが呼び出され、自身のforwardメソッドを実行）
  3. 2の結果を引数に、Linear2の__call__メソッドが呼び出される→linearのforwardメソッドが実行される
2. 1の結果y_pred（予測値）とy（教師データ）を引数にMeanSquaredErrorを実行（内部で__call__メソッドが呼び出され、自身のforwardメソッドを実行）
3. 2の結果lossのbackwardメソッドを呼び出し、各ノードに伝播する勾配を求める
4. 3の結果から、パラメータW1,W2,b1,b2を別途定めた学習率に則り更新する

ステップ45 レイヤをまとめるレイヤ

現状のLayerインスタンスは複数使うにも関わらず別個に管理する必要があります。これらを一元的に管理できるようにするステップです。一気にDeZeroが他の有名なライブラリの様に動くようになりますが、基本的な処理の流れは先ほどの図から大きな変更はありません。

一つ注意したいのは最初にインスタンス化するのがLayerクラスそのものだということです。Functionクラスは常に継承されて利用され、それ自体がインスタンス化されることはありませんでした。Layerクラスも継承されますが、こちらは自身をインスタンス化することがあり得ます。大元のLayerクラスのインスタンス変数に、それを継承したクラス（Linearなど）を格納していくイメージです。こうすることで、パラメーター更新のコードを短縮することができます。

また、書籍では他のライブラリで良く使用するModelクラス（Layerクラスとほとんどの機能は同じで、可視化のコードを追加したもの）を作成し、それを継承してMLPクラスなど汎用的はニューラルネットモデルを作成します。

そこで未だに解決できていないバグにあたりました…ステップ別のGitHubに公開されているコードを実行する（Modelクラスをimportして使う）と問題ないのですが、notebook内でLayerクラスの定義→Modelクラスの定義→TwoLayerNetクラスを定義して学習とするとmodel._paramsに値が何も格納されず学習が進まないんですよね…色々試したところLayerクラスをnotebook内で定義するのではなくimportして使ってやると問題ないので、Modelクラス定義以降の処理は問題なさそうで、notebook内のLayerクラスに問題がありそうなのですがソースコードコピーしてもダメで…クラスをimportして使うのと同じコードを書いて使うでは挙動は同じ思っていたので何が起こっているのかさっぱりです。。

バグが気持ち悪いですが、最後にLayer-Model-MLPクラスの関係性を簡単に図にして次に進もうと思います。

f:id:cha_kabu:20201119154231p:plain

Layerクラスを継承したModelクラスを継承したMLPクラスのインスタンス変数にLayerクラスを継承したLinearクラスがいて…と正直もう頭がこんがらがってきました。。

最後に

だいぶ既存のDeepLearningライブラリの様な実装ができるようになってきました！次は～ステップ48までのまとめを予定。

2020-11-17

ゼロから作るDeep Learning3　フレームワーク編を読む　その⑦ステップ41

はじめに

シリーズ記事の続編で前記事はこちら↓です。 cha-kabu.hatenablog.com

ですが、今回の内容的にはこちら↓の記事との情報の関連性が高いです。 cha-kabu.hatenablog.com

ステップ41 行列の積

行列積を計算するMatMulクラス、そしてそのインスタンス化とforward処理を行ってくれるmatmul関数を実装します。実装コード自体は今までの延長で難しいことは無いのですが、行列積の逆伝播を理解するのが数学苦手にはしんどいです…魔のステップ37に引き続き、適宜書籍よりも低いレベルから情報をまとめていきます。

参考にしたサイト様

以下の先人たちのまとめを参考にさせて頂きました。本記事で紹介する逆伝播の勾配算出方法はどのページとも異なるのですが、とても参考になりました。なお、本記事に誤った情報があった場合は当然ながらすべて私の理解力の無さが原因であり、引用先の皆様の責任は一切ありません。

頭の中に思い浮かべた時には

Pythonと機械学習

Qiita 【機械学習】誤差逆伝播法のコンパクトな説明

Qiita 行列の和と積の誤差逆伝播法の証明

諸注意

まず、以降の説明で混乱しないために以下の用語を抑えておいてください。

	出力1つ	出力複数
入力1つ	（スカラ値）関数	ベクトル値関数
入力複数	多変数（スカラ値）関数	多変数ベクトル値関数

ステップ37のまとめでも、一応多変数ベクトル値関数の微分までをまとめました。今回は行列積なので行列の行列微分…ではありません。というのも未だに良く分かってないのですが、どうやら「行列の行列微分」ってもの自体が存在しないみたいなんですよね（参考：おしえてgoo）。

「行列積の微分なんだから行列を行列で微分できないとダメじゃん！」と思っていたのですが、先にネタバレをしてしまうと、「行列積の微分そのもの」に注目するのではなく、「最終出力 $\displaystyle{L}$ （スカラ）を微分するとはどういうことか？」から考えていって逆伝播時に下流に流す勾配を求めます。図にすると以下の感じです。（matmulは行列積を行う関数、太字の大文字は行列を表します。）

f:id:cha_kabu:20201117000600p:plain

今までの逆伝播実装では、その時点での勾配を直接（数式的に）求め、上流から流れてくる勾配と掛け合わせて下流に流す実装を行ってきました。 $\displaystyle{\frac{\partial L}{\partial x}=\frac{\partial L}{\partial y}\frac{\partial y}{\partial x}}$ の $\displaystyle{\frac{\partial y}{\partial x}}$ を直接求める方法です。一方、今回はこれまでのものとは違い、逆算的に（？） $\displaystyle{\frac{\partial L}{\partial \bf{X}}}$ はどうやって表すことができるか？に向かって数式を組み立てていく方法になります。

その際重要になってくるのが連鎖律です。スカラ値関数の連鎖律は今までも多用してきたので問題ないと思いますが、合成関数に多変数関数やベクトル値関数が含まれる場合の連鎖律についてまとめた後、逆伝播計算について考えていきます。

なお、以降ベクトルや行列を使った表現が出てきますがそれぞれ幾何的なイメージ（ベクトルは矢印、とか）は持たない方が納得しやすいと思います。単純に、「ベクトルや行列の形でまとめて書いた方がスッキリ書けるからそうしているだけ」で、表記のために使っていると割り切らないと頭がごちゃごちゃになっていきます。自分は「行列とベクトルの積は線形写像だからこの計算の意味は…」とか考え始めてドツボに嵌りました。

目次的なもの

諸注意で記載した通り、連鎖律→逆伝播を実際にやってみる流れでまとめていきます。

多変数関数の連鎖律
逆伝播を実際にやってみる

多変数関数の連鎖律

まずは連鎖律についてまとめます。序盤のステップでも連鎖律自体は使われており、見た目同じなので混乱は少ないと思います。ただし、序盤で出ていた連鎖律は単変数関数のものでした。多変数関数になると形は似ているのですが、「総和をとる」点が異なってきます。

簡単な具体例

まずは証明抜きに簡単な二変数関数の連鎖律を例を見ていきます。 $\displaystyle{z}$ を $\displaystyle{u}$ と $\displaystyle{v}$ の関数、 $\displaystyle{u}$ を $\displaystyle{x}$ の関数、 $\displaystyle{v}$ を $\displaystyle{y}$ の関数とします。数式で表すと以下の通りです。

$\displaystyle{ z = f(u,v)\\ u = g(x)\\ v = h(y) }$

この時、 $\displaystyle{z}$ を $\displaystyle{x}$ で偏微分した値は以下の数式で表すことができます。

$\displaystyle{ \dfrac{\partial z}{\partial x}=\dfrac{\partial z}{\partial u}\dfrac{\partial u}{\partial x}+\dfrac{\partial z}{\partial v}\dfrac{\partial v}{\partial x} }$

更に具体的な例で本当に正しそうか見てみます。例えば $u=x^{2}+x+1、v=2y+1$ として、 $\displaystyle{z=u+v=(x^ {2}+x+1)+(2y+1)}$ となる場合を考えます。この $\displaystyle{z}$ を数式的に $\displaystyle{x}$ で偏微分するのは簡単ですね。 $\displaystyle{2x+1}$ になります。この結果を先ほどの連鎖律を使って出した結果と見合わせます。

f:id:cha_kabu:20201117000623p:plain

確かにあっていそうです。

一般化

先ほどの例は二変数に限ったものでした。これを三変数、四変数、…の時にも適用できるように一般化すると、以下の様に表せられます。

$\displaystyle{ fがu_{1},u_{2},...,u_{m}の関数で、u_{1},u_{2},...,u_{m}がxの関数の時、\\ \begin{align} \dfrac{\partial f}{\partial x}=\sum_{j=1}^{m}\dfrac{\partial f}{\partial u_{j}}\dfrac{\partial u_{j}}{\partial x} \tag{1} \end{align} }$

変数がいくつになっても良い様に、多くの変数を $\displaystyle{u_{1},u_{2},...,u_{m}}$ で表しているのが文字に慣れていないと混乱しますが、先ほどの二変数の例で言うと $\displaystyle{u}$ が $\displaystyle{u_{1}}$ に、 $\displaystyle{v}$ が $\displaystyle{u_{2}}$ に対応しています。先ほどの例から $\displaystyle{v}$ が消えて $\displaystyle{u}$ が増えたわけではないのでご注意ください。別々のアルファベットで表そうとしても最大26文字で使い切ってしまうので、仕方なく添え字で区別し、添え字を使うことで総和記号を使って短く書けるようになっているだけです。

こちらの証明については~~難しいので諦めた~~長くなるのでこちらの九州大学の講義ノートなどでご確認ください。

なお、式 $\displaystyle{(1)}$ を見て「二変数関数の例の $\displaystyle{y}$ にあたる様な、 $\displaystyle{x}$ と対になる変数はどこにいったの？」と混乱してしまう人もいるかも知れません。これは式 $\displaystyle{(1)}$ では $\displaystyle{x}$ についての偏微分のみを問題にしており、変数 $\displaystyle{y}$ は単なる定数（ $\displaystyle{x}$ で偏微分すると0）と見なせるからです。 $\displaystyle{y}$ について同じことをやりたければ、式 $\displaystyle{(1)}$ の $\displaystyle{x}$ を $\displaystyle{y}$ と置き換えるだけです。

特殊形

さて、式 $\displaystyle{(1)}$ はある特殊な条件下では実はもっと簡単な形で書くことができます。特殊な条件とは、 $\displaystyle{u_{1}}$ は $\displaystyle{x}$ の関数、 $\displaystyle{u_{2}}$ は $\displaystyle{y}$ の関数、…といった様にそれぞれの $\displaystyle{u}$ が一つの変数しか持たないときです。具体例で見た方が分かりやすいと思うので、 $\displaystyle{u_{1},u_{2},u_{3}}$ がそれぞれ $\displaystyle{x,y,z}$ の一つだけを変数に持つ場合を考えます。

f:id:cha_kabu:20201117000647p:plain

結局残るのは黒字部分になります。そう考えると結局0になる部分も含めて総和をとる必要はないので式 $\displaystyle{(1)}$ の $\displaystyle{\Sigma}$ は無くすことができ、以下の様に書き換えられます。

$\displaystyle{ fがu_{1},u_{2},...,u_{m}の関数で、u_{x}がxだけを変数に持つ関数の時、\\ \begin{align}\dfrac{\partial f}{\partial x}=\dfrac{\partial f}{\partial u_{x}}\dfrac{\partial u_{x}}{\partial x} \tag{1'}\end{align} }$

$\displaystyle{u_{x}}$ は一般的な表記ではないかと思いますが、ここでは「 $\displaystyle{x}$ だけを変数にもつ関数」の意味で使用しています。

こちらの特殊形はあくまで特殊形で、公式というよりかは式 $\displaystyle{(1)}$ の条件を指定しただけのものなのですが、後で出てきますので覚えておいてください。

式の表現を変えてみる

ここまでのところで多変数関数の連鎖律について学びましたのでもう具体的に逆伝播を考えても良いのですが、少し脱線して「これまでの式って書き換えることができるよね」という話です。逆伝播を考える際にも出てくると言えば出てきますが、文字いっぱいで辛ければ飛ばしてください。

式 $\displaystyle{(1)}$ を見直してみると、ベクトルや行列、その内積を使って表記ができることに気づきます。式を見るよりも展開して書いてみた方が分かりやすいかと思いますので、書き下してみます。なお、こちらでは書籍に合わせて出力を行ベクトルとして表し、かつ転置の記号は付けていません。しかしDeepLearning以外の文脈で多変数関数の連鎖律を調べると、出力を列ベクトルで表記していることがほとんどです。結果が縦に並んでいるか横に並んでいるかだけの違いで本質的には同じですが、数式はそれらのものとは異なりますのでご注意ください。

また、変数を $\displaystyle{x,y,z,...}$ で表していると数に限りがあるので、ここからは $\displaystyle{x_{1},x_{2},x_{3}...}$ の形で表すことにします。

f:id:cha_kabu:20201117000710p:plain

画像内最後の数式に注目頂きたいのですが、この式は参照として記載している多変数ベクトル値関数を全微分した式ととても似た形をしています。ただし、（出力を行ベクトルで表したので）右辺の成分が全微分のときのヤコビ行列×変化量の形から、変化量×ヤコビ行列の形に逆転しています。出力を列ベクトルに合わせるとこの逆転は元に戻るのですが、同時にヤコビ行列（緑字部分）は転置の形になります。

出力も多変数だったら（多変数ベクトル値関数の連鎖律）

これまで見てきた数式展開では、出力はスカラ値であることを前提としていました。出力も多変数、すなわち $\displaystyle{f}$ が多変数ベクトル値関数の場合にどうなるかを見てみます。こちらの数式は書き下すと大変なので、コンパクトにまとめます。

f:id:cha_kabu:20201117000740p:plain

黄色のところは参考までに記載しています。赤の行列を $\displaystyle{\bf{W}}$ 、青を $\displaystyle{\bf{V}}$ 、緑を $\displaystyle{\bf{U}}$ と呼ぶならば、 $\displaystyle{\bf{W}_{11}}$ 成分の計算方法はの1行目 $\displaystyle{\bf{V}}$ 成分と緑の行列の1列目成 $\displaystyle{\bf{U}}$ 分の内積で表せられます。

逆伝播を実際にやってみる

少し脱線しましたがいよいよ行列積の逆伝播について考えていきます。

本記事で今まで使用してきた記号体系と変わってしまいますが、書籍と表記を合わせて以下の逆伝播を考えます。ただし行列とベクトルの表記については一部書籍に従わず、行列は大文字の太字、ベクトルは小文字の太字で表すことにします。

※書籍では $\displaystyle{\bf{X}}$ がベクトルの時のことを先に考えていますが、行列について考えれば網羅できるので本記事では省略します。

f:id:cha_kabu:20201117000757p:plain

目標は図の中の $\displaystyle{\frac{\partial L}{\partial \bf{X}}}$ と $\displaystyle{\frac{\partial L}{\partial \bf{W}}}$ がどう計算できるかを考えることです。 $\displaystyle{\frac{\partial L}{\partial \bf{Y}}}$ については、今回上流の計算が無いので実際の値は分かりませんが、実際に逆伝播するときには上流の計算は終わっているはずので既知と仮定します（ $\displaystyle{\frac{\partial L}{\partial \bf{X}}}$ や $\displaystyle{\frac{\partial L}{\partial \bf{W}}}$ を表す計算式の中に残っても良い）。また $\displaystyle{L}$ は最終出力のスカラです。大文字ですが行列ではないのでご注意ください。

前準備① $\displaystyle{\bf{Y}}$ について

逆伝播の前に、順伝播の時に計算される $\displaystyle{\bf{Y}}$ とは何なのか、具体的に見ておきます。順伝播の図から $\displaystyle{\bf{X}}$ と $\displaystyle{\bf{W}}$ の積であることは明らかですが、その各要素の計算は以下の様になります（意味ありげに書いていますが、ただの行列積です）。

$\displaystyle{ \begin{pmatrix} y_{11} & \cdots & y_{1h} & \cdots & y_{1H} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ y_{n1} & \cdots & y_{nh} & \cdots & y_{nH} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ y_{N1} & \cdots & y_{Nh} & \cdots & y_{NH} \\ \end{pmatrix} = \begin{pmatrix} x_{11} & \cdots & x_{1d} & \cdots & x_{1D} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ x_{n1} & \cdots & x_{nd} & \cdots & x_{nD} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ x_{N1} & \cdots & x_{Nd} & \cdots & x_{ND} \\ \end{pmatrix} \begin{pmatrix} w_{11} & \cdots & w_{1h} & \cdots & w_{1H} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ w_{d1} & \cdots & w_{dh} & \cdots & w_{dH} \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ w_{D1} & \cdots & w_{Dh} & \cdots & w_{DH} \\ \end{pmatrix} }$

行列の積の定義から明らかですが、例えば $\displaystyle{y_{11}}$ の計算は $\displaystyle{\bf{X}}$ の1行目成分と $\displaystyle{\bf{W}}$ の一列目成分の内積で計算され、以下の様に表されます。

$\displaystyle{ y_{11}=x_{11}w_{11}+x_{12}w_{21}+…x_{1d}w_{d1}+…x_{1D}w_{D1} }$

これを一般化すると、 $\displaystyle{\bf{Y}}$ の $\displaystyle{nh}$ 成分 $\displaystyle{y_{nh}}$ は以下の様に計算されます。

$\displaystyle{ y_{nh}=\sum_{d=1}^{D}x_{nd}w_{dh} }$

$\displaystyle{n,h}$ は $\displaystyle{\Sigma}$ の中にある変数なので段々数を増やしてループしたくなりますが、今回は $\displaystyle{\Sigma}$ の影響は受けない添え字ですのでご注意ください。 $\displaystyle{y_{nh}}$ をどれかに定めるとそれと一緒に決定的に決まる変数です。 $\displaystyle{\Sigma}$ の影響を受けるのは $\displaystyle{x}$ の列番号と $\displaystyle{w}$ の行番号で、それぞれ常に同じ値 $\displaystyle{d}$ となります。また、仮定された行列のサイズより $\displaystyle{d}$ の最大値は $\displaystyle{D}$ です。

前準備②この記事だけで使う記法の確認

後々の説明を考え、他ではあまり見ないオリジナルの記法を用いたいと思います。行列 $\displaystyle{\bf{A}}$ の1行目成分（行ベクトル）を、 $\displaystyle{\bf{a_1}}$ の形で「太小文字に行番号を表す添え字」で表します。今回出てくる記号について具体的に書くと以下図の通りです。

f:id:cha_kabu:20201117000820p:plain

前準備はここまでです。それでは $\displaystyle{\frac{\partial L}{\partial \bf{X}}}$ と $\displaystyle{\frac{\partial L}{\partial \bf{W}}}$ をどうやって求めるのか、個別に見ていきましょう。

$\displaystyle{\bf{X}}$ 方向に流れる勾配

$\displaystyle{\frac{\partial L}{\partial \bf{X}}}$ を求めていきます。スカラの行列微分ですので、サイズは $\displaystyle{\bf{X}}$ と同じ $\displaystyle{(N \times D)}$ になります。この後どうやってこれを求めていくかですが、 $\displaystyle{\bf{X}}$ の一要素 $\displaystyle{x_{nd}}$ での偏微分 $\displaystyle{\frac{\partial L}{\partial x_{nd}}}$ について考えていき、後でそれを $\displaystyle{\frac{\partial L}{\partial \bf{X}}}$ に拡張します。

$\displaystyle{x_{nd}}$ と添え字が変数の状態だと分かりづらくなってしまうので、下図の通り $\displaystyle{x_{11},x_{12},x_{21}}$ について具体的に見ていって、後から一般化したいと思います。

f:id:cha_kabu:20201117000829p:plain

まず、3つを代表して $\displaystyle{x_{11}}$ で $\displaystyle{L}$ を偏微分する― $\displaystyle{x_{11}}$ が少し動くと $\displaystyle{L}$ はどう変わるのかを求める―際の連鎖律を考えます。連鎖律を考える際、途中で $\displaystyle{\partial \bf{Y}}$ が何かしらの形で中継地点として出てくるのは想像できるかと思いますが、 $\displaystyle{x_{11}}$ は $\displaystyle{\bf{Y}}$ にどのような影響を与えているのでしょうか？

ここで前準備のところで導出した、 $\displaystyle{y_{nh}=\sum_{d=1}^ {D}x_{nd}w_{dh}}$ を思い出してください。 $\displaystyle{x_{nd}}$ の $\displaystyle{d}$ （列方向成分）については総和をとるので多くの $\displaystyle{y}$ に関わりそうですが、 $\displaystyle{x}$ の行方向成分が $\displaystyle{n}$ であれば、 $\displaystyle{y}$ の行方向成分も $\displaystyle{n}$ で決まります。つまり、 $\displaystyle{x_{11}}$ が影響を与えるのは、 $\displaystyle{\bf{Y}}$ の1行目成分 $\displaystyle{\bf{y}_{1}}$ のみということが分かります。そう考えると連鎖律の特殊形が使え（総和記号が不要）、 $\displaystyle{\frac{\partial L}{\partial x_{11}}}$ 他は以下の様に表すことができます。

$\displaystyle{ \dfrac{\partial L}{\partial x_{11}}=\dfrac{\partial L}{\partial {\bf{y}}_{1}}\dfrac{\partial {\bf{y}}_{1}}{\partial x_{11}}\\ \dfrac{\partial L}{\partial x_{12}}=\dfrac{\partial L}{\partial {\bf{y}}_{1}}\dfrac{\partial {\bf{y}}_{1}}{\partial x_{12}}\\ \dfrac{\partial L}{\partial x_{21}}=\dfrac{\partial L}{\partial {\bf{y}}_{2}}\dfrac{\partial {\bf{y}}_{2}}{\partial x_{21}} }$

続いて引き続き $\displaystyle{x_{11}}$ を代表に、連鎖律の際右辺 $\displaystyle{\frac{\partial \bf{y}_{1}}{\partial x_{11}}}$ が何なのかについて考えます。 $\displaystyle{\bf{Y}}$ の1行目成分 $\displaystyle{\bf{y}_{1}}$ を $\displaystyle{x_{11}}$ で偏微分していますが、そもそも $\displaystyle{\bf{y}_{1}}$ はどのように求められるものだったでしょうか。各要素 $\displaystyle{y_{nh}}$ を $\displaystyle{n=1}$ の時に限って考えることになるので、 $\displaystyle{y_{1h}=\sum_{d=1}^ {D}x_{1d}w_{dh}}$ で求められます。そしてそれぞれ $\displaystyle{x_{11}}$ について偏微分するとペアになる $\displaystyle{w_{1h}}$ だけが残ることになり、 $\displaystyle{\frac{\partial \bf{y}_{1}}{\partial x_{11}}=\bf{w}_{1}}$ になります。少しややこしいのでこのことを書き下してみます。

f:id:cha_kabu:20201117000839p:plain

ということで、他も同様に考えて各連鎖律の式は以下の様にアップデートできます。

$\displaystyle{ \dfrac{\partial L}{\partial x_{11}}=\dfrac{\partial L}{\partial \bf{y}_{1}}{\bf{w}}_{1}\\ \dfrac{\partial L}{\partial x_{12}}=\dfrac{\partial L}{\partial \bf{y}_{1}}{\bf{w}}_{2}\\ \dfrac{\partial L}{\partial x_{21}}=\dfrac{\partial L}{\partial \bf{y}_{2}}{\bf{w}}_{1} }$

良い感じに $\displaystyle{\frac{\partial L}{\partial \bf{X}}}$ の各要素が分かってきたので、具体的に行列に落とし込んでみます。繰り返しになりますが $\displaystyle{\frac{\partial L}{\partial \bf{X}}}$ はスカラ $\displaystyle{L}$ を行列 $\displaystyle{\bf{X}}$ で偏微分しているので、スケールは $\displaystyle{(N \times D)}$ であることを思い出しておいてください。

f:id:cha_kabu:20201117000850p:plain

なんだか凶悪な行列に変化しましたね…しかし、実はこれでもうほぼ完成です！変形後の行列の各要素を見てみます。 $\displaystyle{\bf{w}_d}$ の次元数は、 $\displaystyle{\bf{W}}$ の列数に該当するので $\displaystyle{H}$ です。そして $\displaystyle{\frac{\partial L}{\partial \bf{y}_{n}}}$ は偏微分になっているので分かりにくいですがスカラのベクトル微分なので要はベクトルで、次元数は $\displaystyle{\bf{Y}}$ の列数に該当するのでこちらも $\displaystyle{H}$ です。となると、凶悪に見える各要素はただの次元数 $\displaystyle{H}$ のベクトルどうしの内積でしかなく、行列積で表せそうです！パズルの様にどういう行列積で表せられるか考え（慣れてたら一瞬で分かるのでしょうが…）、書いてみます。

f:id:cha_kabu:20201117000858p:plain

だいぶスッキリしました！ $\displaystyle{\frac{\partial L}{\partial \bf{Y}}}$ のサイズは $\displaystyle{(N \times H)}$ 、 $\displaystyle{\bf{W}^ {T}}$ のサイズは $\displaystyle{(H \times D)}$ なので行列積が成り立つ条件も満たしています。さらに $\displaystyle{\frac{\partial L}{\partial \bf{Y}}}$ は上流から流れてくる勾配なので既知、 $\displaystyle{\bf{W}^ {T}}$ も順伝播の時に使用するものを転置しただけなので既知でしたので、無事 $\displaystyle{\bf{X}}$ 方向の下流に計算可能な勾配を流すことができることが分かりました。

$\displaystyle{\bf{W}}$ 方向に流れる微分

続いて $\displaystyle{\frac{\partial L}{\partial \bf{W}}}$ を求めますが、求め方としては $\displaystyle{\frac{\partial L}{\partial \bf{X}}}$ と同様の考えで求めることができます。しかしまた同じような話を書いてもしょうが無いので、少しズルをします。先ほど求めた通り、 $\displaystyle{\frac{\partial L}{\partial \bf{X}}=\frac{\partial L}{\partial \bf{Y}}{\bf{W}}^ {T}}$ です。また、 $\displaystyle{\bf{Y=XW}}$ であり、転置の性質より $\displaystyle{\bf{Y^ {T}=W^ {T}X^ {T}}}$ です。これを求めたものに対応させて置き換えて求めます。図で書くと以下の様な感じです。

f:id:cha_kabu:20201117000907p:plain

こちらも既知の成分で表すことができました！

最後に

以上でステップ41のまとめ終了です。ステップ37と合わせて1週間くらい時間かかりました…個人的な一番の学びは、「テンソル微分は意味は考えずに"そう表せるからそうしてるだけ"と考えた方が分かりやすい」です。なんちゃら写像やらなんりゃら座標やらの知識を中途半端に掻い摘んで沼に嵌っていきました…次のステップからはスピード上げていきたいところです。

はじめに

MOA

スパムメール判別コンペ

Solafune

atmacup08

終わりに

はじめに

本編

ステップ55-56 CNNのメカニズム

出力サイズの計算方法

3～４階テンソルの畳み込み演算による形状変化

ステップ57 conv2d関数とpooling関数

im2col関数

N=C=KN=1の場合：素朴なim2col

N=C=KN=1の場合：改良版im2col

N,C,KN > 1の場合：素朴なim2col

N,C,KN > 1の場合：改良版im2col

im2colまとめ

conv2d関数

pooling関数

代表的なCNN（VGG16）

最後に

はじめに

本編

ステップ52 GPU対応

ステップ53 モデルの保存と読み込み

ステップ54 Dropoutとテストモード

最後に

はじめに

本編

ステップ49 Datasetクラスと前処理

ステップ50 ミニバッチを取り出すDataLoader

ステップ51 MNISTの学習

最後に

はじめに

本編

ステップ46 Optimizerによるパラメター更新

WeightDecay

ClipGrad

FreezeParam

ステップ47 ソフトマックス関数と交差エントロピー誤差

ソフトマックス関数

交差エントロピー誤差

ステップ48 多値分類

最後に

はじめに

本編

ステップ42 線形回帰の理論

ステップ43 ニューラルネットワークの実装

パラメータをまとめるレイヤ

特殊メソッド__setattr__

yield

クラスのまとめ

ステップ45 レイヤをまとめるレイヤ

最後に

はじめに

ステップ41 行列の積

参考にしたサイト様

諸注意

目次的なもの

多変数関数の連鎖律

簡単な具体例

一般化

特殊形

式の表現を変えてみる

出力も多変数だったら（多変数ベクトル値関数の連鎖律）

逆伝播を実際にやってみる

前準備①について

前準備②この記事だけで使う記法の確認

方向に流れる勾配

方向に流れる微分

最後に

特殊メソッドsetattr

前準備① $\displaystyle{\bf{Y}}$ について

$\displaystyle{\bf{X}}$ 方向に流れる勾配

$\displaystyle{\bf{W}}$ 方向に流れる微分