ゼロから作るDeep Learning3 フレームワーク編を読む その⑫ステップ55~58
はじめに
以下の記事シリーズの続きです。
本編
ステップ55-56 CNNのメカニズム
ほとんどコードは無く、CNN自体の説明です。実装についてはステップ57でまとめて行われるので、特に苦手なところだけまとめておきます。
出力サイズの計算方法
いつも計算時にいったん考えないと出てこない…数式で書くと↓
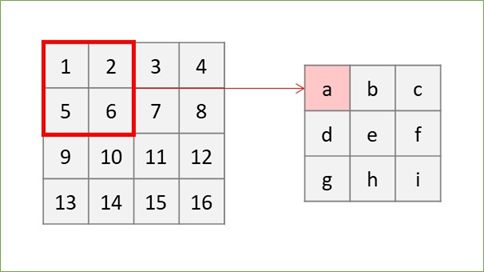
で、日本語で書くと「アウトプットのサイズは"入力サイズにパディングの2倍を足してフィルタサイズを引いたものをストライドで割って1を足して"求める」ですが、今回こちらのQiita記事の説明を見て頭に染み付いた気がします!画像借用します。
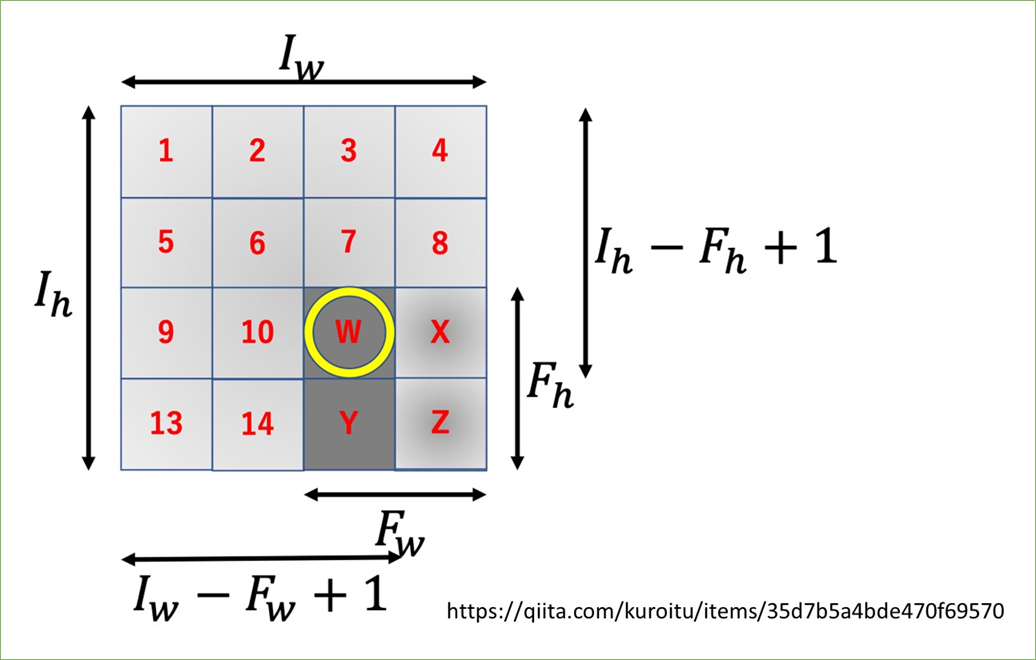
この図が言っているのは、「(パディングやストライドを考えなければ)一番最後にフィルタを掛けた時のフィルタの左上、画像でいうとWのインデックスが出力行列のサイズになる」ということです。この場合Wは3行3列にいるので出力も3*3になります。
これをベースにしつつ、
- パディングは両端が増えるから
を足す
- ストライドはフィルタを1マスごとにかけるのを基準にすると反比例的に回数が減っていくので
で割る(
以外)
を思い出せば忘れずにいられそうです…!
3~4階テンソルの畳み込み演算による形状変化
分からなくはないですがこちらもパッと出てこないので書籍のまんまですがメモって覚えます。まずは3階テンソルの場合。
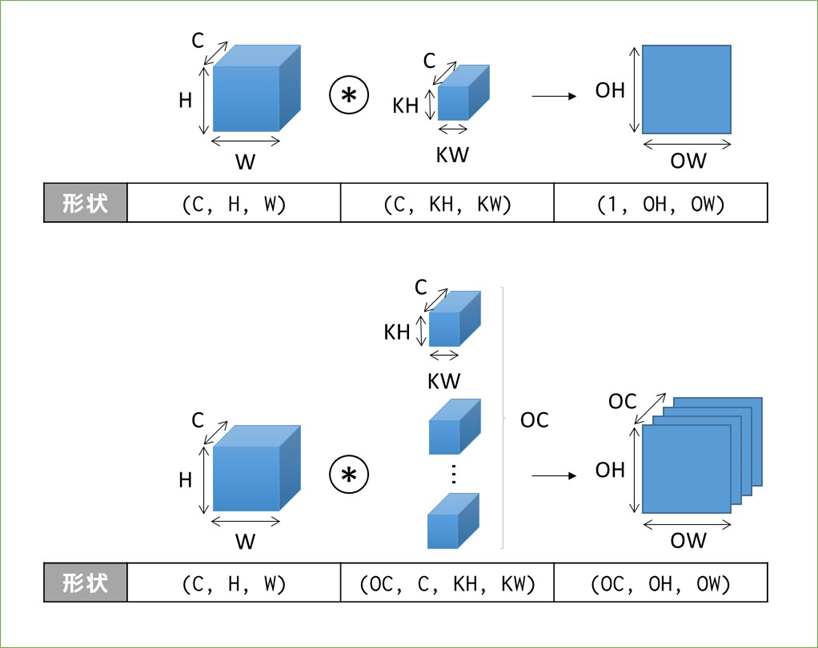
これにバイアスが足されることもありますが、Outputのサイズは変わりません。続いて4階テンソル(ミニバッチ処理)の場合。
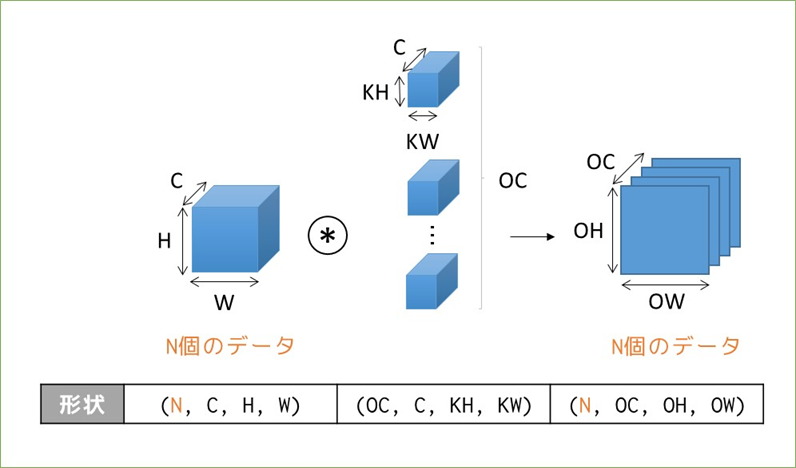
表現の順番としては(バッチサイズ, チャンネル数, 高さ, 幅)の順で、フィルタは毎回同じものが適用されるので「N個のデータ」という概念がない点がいっつもややこしいです。。
ステップ57 conv2d関数とpooling関数
いよいよ実装です。タイトルの関数の他、書籍で説明がないim2colもまとめていきたいと思います。
im2col関数
DeZeroのfunctions_convモジュールにある、Functionを継承したクラスです。クラスそのものよりもforward処理で呼び出しているim2col_array関数の理解が重要です。この関数が何をやっているかをざっくりと言うと「画像を(工夫して)行列に変換」しています。何でわざわざそんなことをするかというと、「その方がnumpyの計算効率が良いから」です。行列に変換される過程と、少し先取りして畳み込み演算が行われる様子も合わせて図にまとめていきます。
まずこれからやることの全体像です。※先ほどまでは書籍に則ってブロックで考えていましたが、以降は平面で考えることにします。ブロックで考えると概要は掴めるのですが、「実際に各値がどうなっているのか?」を掴むには平面で考えた方が良いと思います。
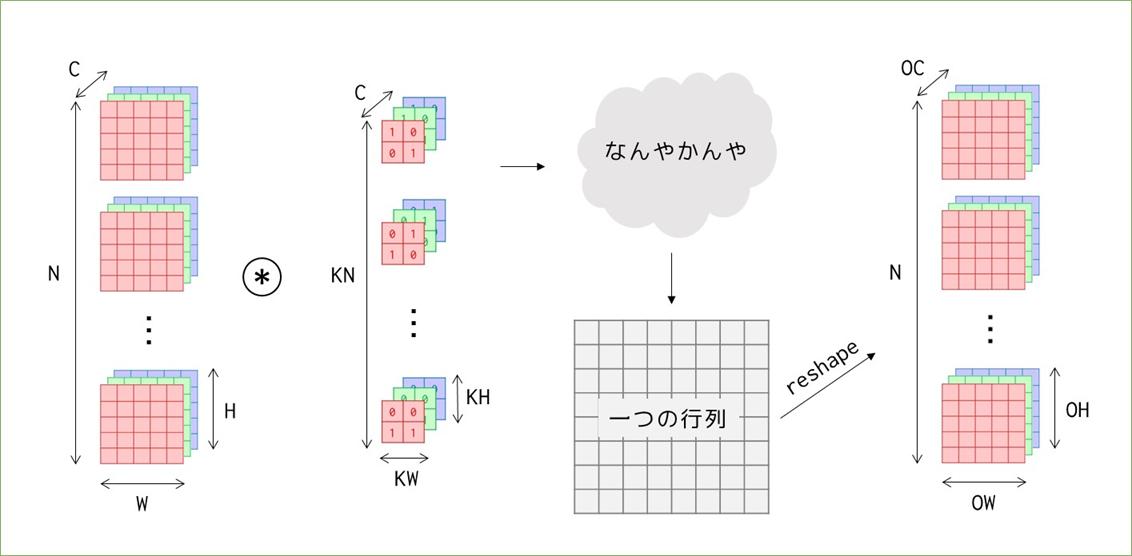
(N, C, W, H)の画像に、(KN, C, KW, KH)のカーネルを適用し最終的には特徴マップを出力に得ます。覚えておきたいのは、途中の「なんやかんや」の計算によって特徴マップの前(と、実は画像とカーネルの要素積を行う前)に、バッチ数やチャンネル数に関わらず一つの大きな行列が出来上がるということを覚えておいてください。
N=C=KN=1の場合:素朴なim2col
まずは簡単なパターンから、バッチサイズ1、チャンネル数1のグレー画像4×4に2×2のカーネルを適用することを考えます。im2colを考えない畳み込み演算は以下の様にカーネルと画像の該当箇所の要素積で出力が求められます。
この計算をどうやって行うかというと、無理くりfor文を繰り返すことでもできますが、その場合一か所辺りカーネルのマス数4回×9回移動=36回のループ計算が必要になります1。一方以下のように考えると行列積で考えられ、計算量を削減できます。
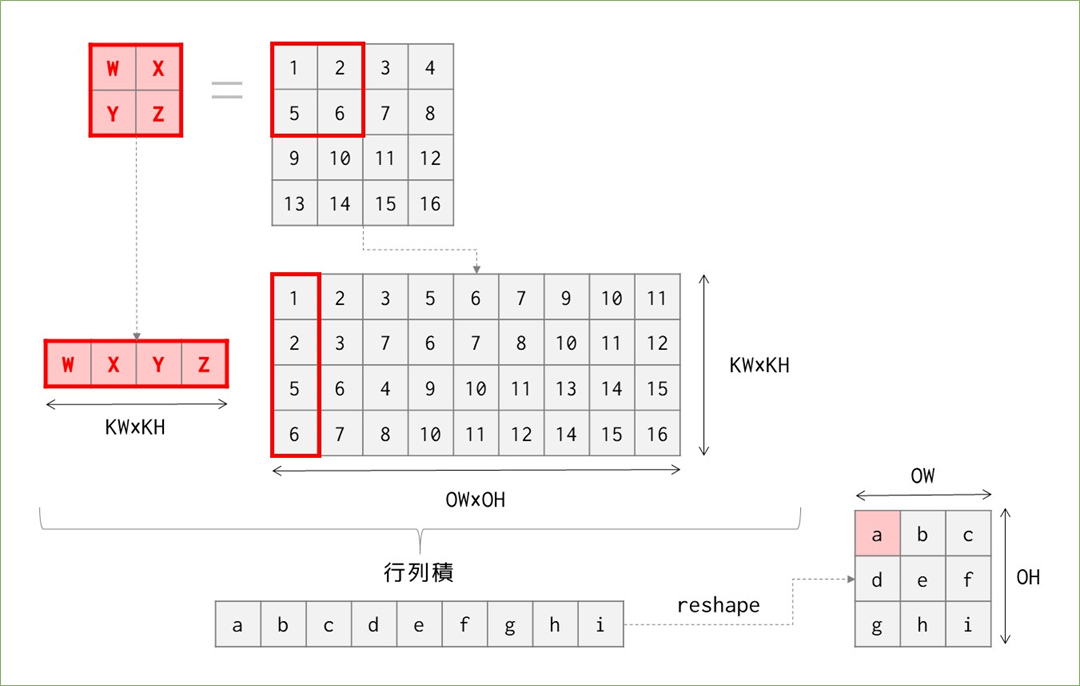
図の4*4の画像を4*9に変換しているところが素朴版im2colがやっていることです。これにより、計算量は"ほぼ"(実際にはカーネルの変換、行列積、reshapeで各1回必要なので"ほぼ"です)画像の変換回数(カーネルが動く回数)分で済むので、36回→9回に納めることができました。以上、im2colの説明!…とはならず、改善が考えられます。
N=C=KN=1の場合:改良版im2col
結論を先に言うと、先ほどまでの計算方法では計算量は出力の要素分だけ必要だったのに対し、これから行う方法では出力のサイズに関わらず、カーネルの要素数分だけのループ計算で済みます。イメージとしては、先ほどの図では画像の変換をカーネルを1マスずつ動かして縦に並べることを繰り返していたところ、今度は出力のサイズのマスを動かしながら横に並べていきます。
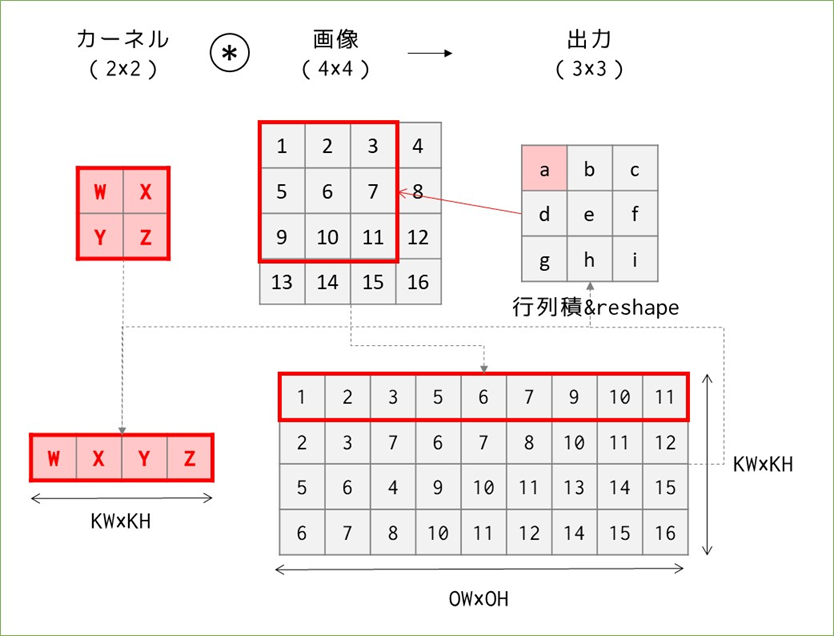
図にすると↑の様な形で、先ほどまでと違って出力のサイズを先に見て、同サイズのカーネル"もどき"を画像の中で動かして要素を横に並べます。これでも変換後の行列は先ほどと同じものになっているので、後は先ほど同様にカーネルを横に並べたものとの行列積を求めてreshapeすると出力を得ることができます。行列積とreshapeを除けば、計算量は36→9→4回まで減りました。
この改良の凄いところは、計算量がKW×KH=カーネルの要素数で済むということで、元の画像のサイズに関係なく計算量を一定に保てます。※パディングやストライドは無視した話です。
N,C,KN > 1の場合:素朴なim2col
続いてバッチ処理とRGB画像を扱う場合を考えます。まずはim2colを使わずに、畳み込みだけを考える場合です。
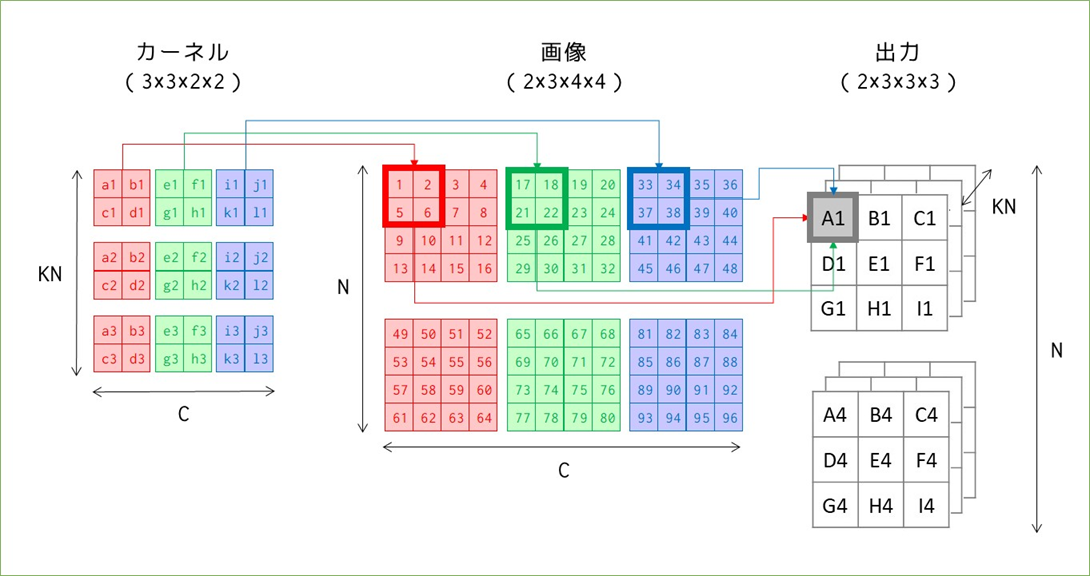
変化があったところだけ記号を付けています。カーネルと画像は同じチャンネル数3を持っており、これは出力のサイズに影響を与えていません。ただし、出力の1マスの計算が1カーネルマス分の積の和だったのに対し、3チャンネル分のカーネルマス分の積の和になっています(A1で例示)。
カーネル数KNは、出力のチャンネル数と対応しています。出力のチャンネル数はカーネルと画像のチャンネル数ではなく、カーネル数に左右されるというのが少し分かりにくいです。図では表せていませんが、A1~I1の出力の後ろにはA2~I2の出力が並んでおり、その計算は2つ目のカーネルと1つ目の画像で行われます。
画像のバッチサイズNは出力のデータ数と一致します。2つ目の画像49~96と3つのカーネルすべてを使って2つ目の出力を得ます。
この計算量は合っている自信はありませんが…最初のグレーチャンネルの36回をベースに、3チャンネル分×2バッチ分の6倍必要なので、216回のループ処理が必要になります。2
これも先ほどの例と同様にim2colを使うと行列演算をすることができます。
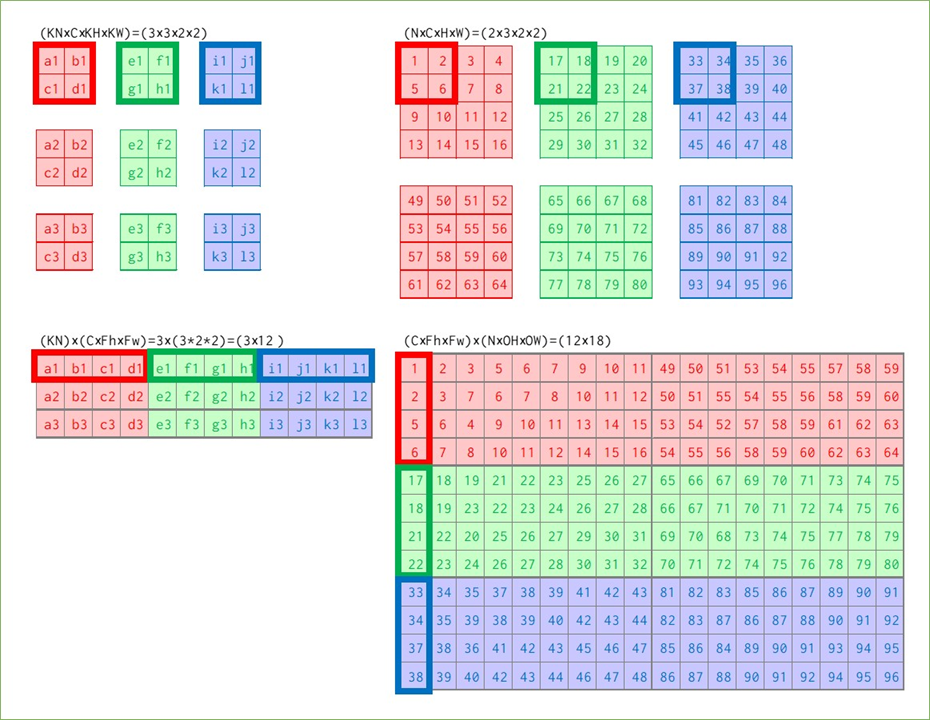
細かすぎて見えない&スペースの問題で出力を省略していますが…行列の並べ方に注意してください。カーネルは横にチャンネル、縦に種類を並べており、画像は横に種類、縦にチャンネルを並べています。小さく各サイズを書いていますが、カーネルは(3×12)、画像は(12×18)の行列となり、(3×18)の出力(reshape前)を得ます。先ほど単純な畳み込みで見たときの出力の総マス数は9*3*2=54マスで、今回は3*18=54マスなので、reshapeすれば同じ出力を得られることが想像できます。
この場合の計算量は、ほぼカーネルと画像の変換回数だと考えると、カーネルは単純に9個を横に並べるだけなので9回、画像は1つあたり9回の移動がありそれが6個あるので9*6=54回で合計9+54=63回のループで計算できます。216回よりかはだいぶ少なくなりましたが、先ほどと同様の方法で削減できます。
N,C,KN > 1の場合:改良版im2col
小見出しが嘘になってしまうのですが、効率的に並べる方法は1チャンネルの時と同じなので省略します。計算量としてはカーネルのマス数=4マス/個でカーネルが全部で9個あるので36回の計算で済みます。
改良版だけではなく素朴版も同じですが先ほど画像に入りきらなかった出力への変換を見てみます。

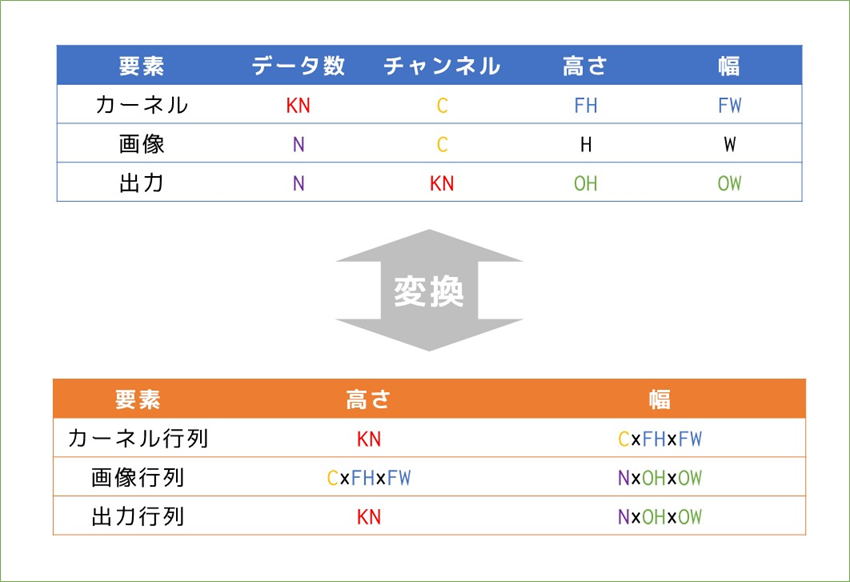
先ほど説明した通り、(3×12)のカーネル行列と(12×18)の画像行列の行列積をとると(3×18)の出力行列ができ、それをreshapeして出力(2×3×3×3)を得ます。
im2colまとめ
これまで見てきたことをアルゴリズムとして実装するためのim2col関数の中身は、素人には厳しいコードとなっています…。しかし「使う」という観点ではこれまで見てきた様に各要素のサイズがどう変換されているか、何が対応しているかを覚えておくことの方が重要かと思うので、最後にそれをまとめてim2colは終わりにしておきます。そしてここまで書いて気付いたのですが書籍の実装や説明に対して高さと幅すべて転置の状態で説明していましたね…しかし説明を修正するのも面倒なのでこのままいきます。。形が転置(高さと幅が入れ替わる&行列積の際に画像とカーネルの位置関係が変わる)になるだけでやっていることは同じです!
im2colと畳み込み演算によって、カーネルと画像が行列に変換され出力を行列で得て、それをreshape(はたまたcol2im)によって再度変換して最終出力を得ます。
また、ここまでストライド1固定でパディングのことは考えずにやってきましたが、長くなってしまったのとそれらもim2colを使う際にはパラメータ設定だけで意識せずで良さそうなので先に進みます…
conv2d関数
行われることはim2colと一緒に説明しました。書籍で紹介されているconv2d_simple関数についてはカーネルをreshapeしたりtransposeしたりしていますが、先ほど説明したことの実装です。関数の中身を分解して使って、先ほどの具体例と同じ結果になるかだけ見てみます。
先に補足しますと、先ほど説明した具体例と形状を合わせるため、一部書籍とコードが異なります。また、出力行列を正しく出力に戻せているか確認するためカーネルの重みは3個それぞれ0.1,0.2,0.3として、事前にExcelで計算した結果とあっているか確認します。
import numpy as np import dezero.functions as F # 入力(画像ダミー)の作成:(N×C×H×W)=(2×3×4×4) x = np.arange(1,97).reshape(2,3,4,4) # カーネル(重み)の作成:(KN×C×KH×KW)=(3×3×2×2) w1, w2, w3 = np.full((3,2,2),0.1), np.full((3,2,2),0.2), np.full((3,2,2),0.3) W = np.array([w1,w2,w3]) print(W.shape) #(3, 3, 2, 2) # 入力にim2colを適用→書籍と逆に説明していたので転置 col = F.im2col(x,(2,2)).transpose() print(col.shape) # (12, 18) # カーネルはreshapeで変形→書籍と逆に説明していたので転置しない W = W.reshape(3,-1) print(W.shape) # (3, 12) # 行列積(linear関数を適用)で出力行列を求める t = F.linear(W, col, b=None) print(t.shape) # (3, 18) # 出力の形にreshape:(N×KN×OH×OW) t.T.reshape(2,3,3,3).transpose(0,3,1,2)
結果の数字に意味は無いので省略しますが、事前の計算結果と一致しました。
続いて書籍ではConv2dレイヤを実装しますが、やっているのは__init__()で主にconv2d_simple関数に渡すインスタンス変数を宣言、_init_W()で初回のカーネルの重みを初期化し、forward()では初回は_init_W()を呼び出しあとはconv2d_simple関数を呼び出して出力を返すだけです。
pooling関数
maxプーリングを行う関数の実行です。実施内容は全く異なりますがコードとしてはconv2d_simple関数と似通っている(出力にim2colを適用して行列化→reshape→行方向に最大値を求める→reshapeして出力)のでここまでを理解できていれば特に難しくないと思います。
代表的なCNN(VGG16)
VGG16クラスの実装については画像処理を行ったことがあれば意味は分かると思います。ここでは各処理を行ったときのサイズを確認しておきたいと思います。入力画像のサイズは(10, 3, 224, 224)を仮定しています。
| __init__() | forward() | サイズ |
|---|---|---|
| self.conv1_1 = L.Conv2d(64, kernel_size=3, stride=1, pad=1) | x = F.relu(self.conv1_1(x)) | (10, 64, 224, 224) |
| self.conv1_2 = L.Conv2d(64, kernel_size=3, stride=1, pad=1) | x = F.relu(self.conv1_2(x)) | (10, 64, 224, 224) |
| x = F.pooling(x, 2, 2) | (10, 64, 112, 112) | |
| self.conv2_1 = L.Conv2d(128, kernel_size=3, stride=1, pad=1) | x = F.relu(self.conv2_1(x)) | (10, 128, 112, 112) |
| self.conv2_2 = L.Conv2d(128, kernel_size=3, stride=1, pad=1) | x = F.relu(self.conv2_2(x)) | (10, 128, 112, 112) |
| x = F.pooling(x, 2, 2) | (10, 128, 56, 56) | |
| self.conv3_1 = L.Conv2d(256, kernel_size=3, stride=1, pad=1) | x = F.relu(self.conv3_1(x)) | (10, 256, 56, 56) |
| self.conv3_2 = L.Conv2d(256, kernel_size=3, stride=1, pad=1) | x = F.relu(self.conv3_2(x)) | (10, 256, 56, 56) |
| self.conv3_3 = L.Conv2d(256, kernel_size=3, stride=1, pad=1) | x = F.relu(self.conv3_3(x)) | (10, 256, 56, 56) |
| x = F.pooling(x, 2, 2) | (10, 256, 28, 28) | |
| self.conv4_1 = L.Conv2d(512, kernel_size=3, stride=1, pad=1) | x = F.relu(self.conv4_1(x)) | (10, 512, 28, 28) |
| self.conv4_2 = L.Conv2d(512, kernel_size=3, stride=1, pad=1) | x = F.relu(self.conv4_2(x)) | (10, 512, 28, 28) |
| self.conv4_3 = L.Conv2d(512, kernel_size=3, stride=1, pad=1) | x = F.relu(self.conv4_3(x)) | (10, 512, 28, 28) |
| x = F.pooling(x, 2, 2) | (10, 512, 14, 14) | |
| self.conv5_1 = L.Conv2d(512, kernel_size=3, stride=1, pad=1) | x = F.relu(self.conv5_1(x)) | (10, 512, 14, 14) |
| self.conv5_2 = L.Conv2d(512, kernel_size=3, stride=1, pad=1) | x = F.relu(self.conv5_2(x)) | (10, 512, 14, 14) |
| self.conv5_3 = L.Conv2d(512, kernel_size=3, stride=1, pad=1) | x = F.relu(self.conv5_3(x)) | (10, 512, 14, 14) |
| x = F.pooling(x, 2, 2) | (10, 512, 7, 7) | |
| x = F.reshape(x, (x.shape[0], -1)) | (10,25088) | |
| self.fc6 = L.Linear(4096) | x = F.dropout(F.relu(self.fc6(x))) | (10,4096) |
| self.fc7 = L.Linear(4096) | x = F.dropout(F.relu(self.fc7(x))) | (10,4096) |
| self.fc8 = L.Linear(1000) | x = self.fc8(x) | (10,1000) |
基本的なことですが、以下の様にサイズが変化しています。
- Conv2dレイヤを通るとチャネル数が変化する(かそのまま)
- pooling関数を通すとHとWが半分になる
- reshapeでNを保持して行列に変換する:サイズが(N, C×H×W)になる
- 全結合層を通して行列のサイズを(10, 4096)に小さくして
- 最後に(N, 1000)にする。1,000は学習済みモデルの分類数なので、学習済みモデルを使用しない場合は適宜変更する。
以降の使い方はお作法的なものはありますが内容は難しくないかと思います。
最後に
おそらく次で最後!何とか初期に考えていた1か月で読破できそうです。